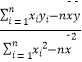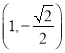题目内容
【题目】对于![]() 维向量
维向量![]() ,若对任意
,若对任意![]() 均有
均有![]() 或
或![]() ,则称
,则称![]() 为
为![]() 维
维![]() 向量. 对于两个
向量. 对于两个![]() 维
维![]() 向量
向量![]() 定义
定义![]() .
.
(1)若![]() , 求
, 求![]() 的值;
的值;
(2)现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,求证:该序列中不存在
,求证:该序列中不存在![]() 维
维![]() 向量
向量![]() .
.
(3) 现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,若存在正整数
,若存在正整数![]() 使得
使得![]() 为
为![]() 维
维![]() 向量序列中的项,求出所有的
向量序列中的项,求出所有的![]() .
.
【答案】(1)![]() (2)不存在(3)
(2)不存在(3)![]()
【解析】试题分析:(Ⅰ)根据![]() 的定义可求得其值;(Ⅱ)利用反证法,向量
的定义可求得其值;(Ⅱ)利用反证法,向量![]() 的每一个分量变为
的每一个分量变为![]() ,都需要奇数次变化,根据
,都需要奇数次变化,根据![]() ,得出矛盾;(Ⅲ)根据题意可得
,得出矛盾;(Ⅲ)根据题意可得![]() .
.
试题解析:(Ⅰ)由于![]() ,
, ![]() ,由定义
,由定义![]() ,
,
可得![]() .
.
(Ⅱ)反证法:若结论不成立,即存在一个含![]() 维
维![]() 向量序列
向量序列![]() ,
,
使得![]() ,
, ![]() .
.
因为向量![]() 的每一个分量变为
的每一个分量变为![]() ,都需要奇数次变化,
,都需要奇数次变化,
不妨设![]() 的第
的第![]() 个分量
个分量![]() 变化了
变化了![]() 次之后变成
次之后变成![]() ,
,
所以将![]() 中所有分量
中所有分量![]() 变为
变为![]() 共需要
共需要![]()
![]() 次,此数为奇数.
次,此数为奇数.
又因为![]() ,说明
,说明![]() 中的分量有
中的分量有![]() 个数值发生改变,
个数值发生改变,
进而变化到![]() ,所以共需要改变数值
,所以共需要改变数值![]() 次,此数为偶数,所以矛盾.
次,此数为偶数,所以矛盾.
所以该序列中不存在![]() 维
维![]() 向量
向量![]() .
.
(Ⅲ)此时![]() .
.

练习册系列答案
相关题目