题目内容
【题目】
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分,不低于85分称优秀)人数之间的关系进行分析研究,他们从本校初二,初三,高一,高二,高三年级各随机抽取了40名学生,记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数,得到如下数据表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工(单位:小时) | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y(单位:人) | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,再用剩下的2组数据进行检验.
(1)若选取的是初三,高一,高二的3组数据,请根据这3组数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?
参考数据:![]() ,
,![]() .
.
参考公式: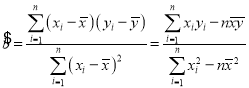 ,
,![]() .
.
【答案】(1)![]()
(2)可靠
【解析】
(1)根据条件计算出![]() 、
、![]() ,从而求出
,从而求出![]() ,
,![]() ,即可求出回归方程.
,即可求出回归方程.
(2)代入回归方程计算可得.
解:(1)∵![]() ,
,
![]() .
.
 .
.
![]() .
.
∴y关于x的线性回归方程为![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() .
.
由此分析,(1)中得到的线性回归方程是可靠的.

【题目】某客户准备在家中安装一套净水系统,该系统为三级过滤,使用寿命为十年.如图所示,两个一级过滤器采用并联安装,二级过滤器与三级过滤器为串联安装。

其中每一级过滤都由核心部件滤芯来实现。在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立),三级滤芯无需更换,若客户在安装净水系统的同时购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.若客户在使用过程中单独购买滤芯,则一级滤芯每个
元.若客户在使用过程中单独购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据
元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据![]() 套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据
套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据![]() 个一级过滤器更换的滤芯个数制成的柱状图,表是根据
个一级过滤器更换的滤芯个数制成的柱状图,表是根据![]() 个二级过滤器更换的滤芯个数制成的频数分布表.
个二级过滤器更换的滤芯个数制成的频数分布表.

二级滤芯更换频数分布表
二级滤芯更换的个数 |
|
|
频数 |
|
|
以![]() 个一级过滤器更换滤芯的频率代替
个一级过滤器更换滤芯的频率代替![]() 个一级过滤器更换滤芯发生的概率,以
个一级过滤器更换滤芯发生的概率,以![]() 个二级过滤器更换滤芯的频率代替
个二级过滤器更换滤芯的频率代替![]() 个二级过滤器更换滤芯发生的概率.
个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为![]() 的概率;
的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() ,
,![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() ,
,![]() 的值.
的值.
【题目】2019年春节档有多部优秀电影上映,其中《流浪地球》是比较火的一部.某影评网站统计了100名观众对《流浪地球》的评分情况,得到如下表格:
评价等级 | ★ | ★★ | ★★★ | ★★★★ | ★★★★★ |
分数 | 0~20 | 2140 | 4160 | 61~80 | 81100 |
人数 | 5 | 2 | 12 | 6 | 75 |
(1)根据以上评分情况,试估计观众对《流浪地球》的评价在四星以上(包括四星)的频率;
(2)以表中各评价等级对应的频率作为各评价等级对应的概率,假设每个观众的评分结果相互独立.
(i)若从全国所有观众中随机选取3名,求恰有2名评价为五星1名评价为一星的概率;
(ii)若从全国所有观众中随机选取16名,记评价为五星的人数为X,求X的方差.

