题目内容
12.(1)作出函数f(x)=|x+3|+|x-3|的图象,并指出函数f(x)的单调区间;(2)作出函数f(x)=|x+3|-|x-3|的图象,并指出函数f(x)的单调区间.
分析 (1)化简函数的解析式,然后画出图象即可.找出单调区间.
(2)去掉绝对值符号化简函数的解析式,然后画出图象.指出函数f(x)的单调区间.
解答 解:(1)函数f(x)=|x+3|+|x-3|=$\left\{\begin{array}{l}2x,x≥3\\ 6,-3<x<3\\-2x,x≤-3\end{array}\right.$,函数的图象如图: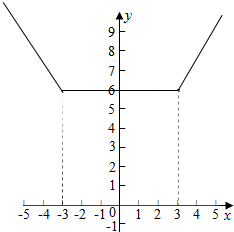
,函数f(x)的单调增区间[3,+∞)减区间:(-∞,-3];
(2)函数f(x)=|x+3|-|x-3|=$\left\{\begin{array}{l}6,x≥3\\ 2x,-3<x<3\\-6,x≤-3\end{array}\right.$,函数的图象如图: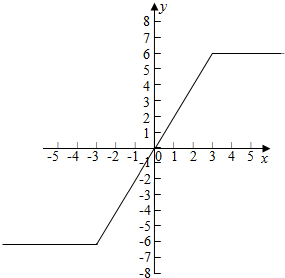 ,
,
函数f(x)的单调增区间:[-3,3].
点评 本题考查分段函数的应用,函数的图象的作法,单调区间的求法,考查计算能力.

练习册系列答案
相关题目
17.设函数f(x)=x2-3x+1,则f(a)-f(-a)=( )
| A. | 0 | B. | -6a | C. | 2a2+2 | D. | 2a2-6a+2 |
 如图,已知四棱锥P-ABCD,ABCD为正方形,PA⊥平面ABCD,给出下列命题:
如图,已知四棱锥P-ABCD,ABCD为正方形,PA⊥平面ABCD,给出下列命题: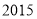 年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取
年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取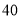 名学生的数学成绩进行统计,将他们的成绩分成六段
名学生的数学成绩进行统计,将他们的成绩分成六段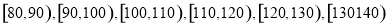 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.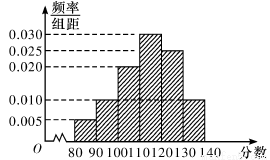
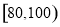 内的学生中任意抽取2人,求成绩在
内的学生中任意抽取2人,求成绩在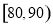 中至少有一人的概率.
中至少有一人的概率.