题目内容
3.F1,F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,过F2作直线交椭圆于A,B两点,已知AF1⊥BF1,∠ABF1=30°,则椭圆的离心率为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}-\sqrt{3}}{2}$ | C. | $\sqrt{6}$-$\sqrt{2}$ | D. | $\sqrt{6}$-$\sqrt{3}$ |
分析 如图所示,设|AF1|=m.利用直角三角形的边角关系、椭圆的定义可得m=$\frac{2a(3-\sqrt{3})}{3}$.在△AF1F2中,由余弦定理可得:(2c)2=m2+(2a-m)2-2m(2a-m)cos60°,
化简利用离心率计算公式即可得出.
解答 解:如图所示, 设|AF1|=m.
设|AF1|=m.
∵AF1⊥BF1,∠ABF1=30°,
∴|AB|=2m,|AF2|=2a-m,
|BF1|=$\sqrt{3}$m,|BF2|=2m-(2a-m)=3m-2a,
∴$\sqrt{3}$m+3m-2a=2a,
解得m=$\frac{4a}{3+\sqrt{3}}$=$\frac{2a(3-\sqrt{3})}{3}$.
∴3m2=$(16-8\sqrt{3}){a}^{2}$,
6am=$(12-4\sqrt{3}){a}^{2}$.
在△AF1F2中,由余弦定理可得:(2c)2=m2+(2a-m)2-2m(2a-m)cos60°,
化为4c2-4a2+6am-3m2=0,
∴4c2-4a2+$(12-4\sqrt{3}){a}^{2}$-$(16-8\sqrt{3}){a}^{2}$=0,
化为${e}^{2}=2-\sqrt{3}$,
∴e=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
故选:A.
点评 本题考查了直角三角形的边角关系、椭圆的定义及其性质、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
13.已知甲、乙二人决定各购置一辆纯电动汽车,甲从A、B、C三类车型中挑选,乙只从B、C两类车型中挑选,甲、乙二人选择各类车型的概率如下表:
若甲、乙两人都选C类车型的概率为$\frac{1}{3}$.
(1)求p1、p2的值;
(2)该市对购买纯电动汽车进行补贴,补贴标准如下表:
记甲、乙两人购买所获得的财政补贴(单位:万元)的和为X,求X的数学期望E(X).
| 车型 概率 人 | AA | BB | CC |
| 甲 | $\frac{1}{6}$ | p1 | p2 |
| 乙 | / | $\frac{1}{3}$ | $\frac{2}{3}$ |
(1)求p1、p2的值;
(2)该市对购买纯电动汽车进行补贴,补贴标准如下表:
| 车型 | A | B | C |
| 补贴金额(万元) | 1 | 2 | 3 |
 一个四棱椎的三视图如图所示
一个四棱椎的三视图如图所示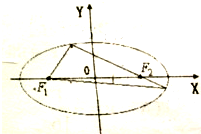 设点F1,F2是$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1的两个焦点,过F2的直线l与椭圆相交于A、B两点.
设点F1,F2是$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1的两个焦点,过F2的直线l与椭圆相交于A、B两点.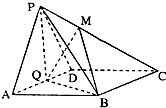 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.