��Ŀ����
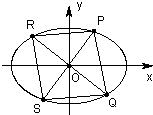 ��֪��ԲC��
��֪��ԲC��| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
��1������Բ�ķ��̣�
��2��������Բ���ҽ��㣬��б��Ϊ
| �� |
| 3 |
��3����ͼ����ԭ�����ֱ������ֱ������Բ
| x2 |
| 4 |
| y2 |
| 2 |
| �� |
| 2 |
��������1��������Բ�����ʣ���֪���㵽����������˵�ľ���ֱ�Ϊa+c��a-c���ٰ�������ֵ���룬���ɵó�a��b��ֵ�������Բ�ķ��̣�
��2�������ҳ���ʽ���㼴�ɣ�ע���������˼������ã�
��3���ȼ��裺��PSQ��Ϊ�������Σ���ֱ��PS�ķ��̣���ֱ��RQ�ķ���Ҳ��֪���ֱ�����Բ���������������ҳ���ʽ���PS��OQ�ij��ȣ��ٸ������������еĹ�ϵ�жϼ��ɣ�
��2�������ҳ���ʽ���㼴�ɣ�ע���������˼������ã�
��3���ȼ��裺��PSQ��Ϊ�������Σ���ֱ��PS�ķ��̣���ֱ��RQ�ķ���Ҳ��֪���ֱ�����Բ���������������ҳ���ʽ���PS��OQ�ij��ȣ��ٸ������������еĹ�ϵ�жϼ��ɣ�
����⣺��1���������
�����a=2��c=
��b=1
����ķ���Ϊ
+y2=1
��2��ֱ�߷���Ϊy=
(x-
)��
������Բ���̵�13x2-24
x+32=0������
��
���ҳ���ʽ���AB=
��
��3����P��y���ϣ�Q��x����ʱ����PSQ�����������Σ�
��P����y����ʱ����ֱ��PS��б��Ϊk��P��x1��kx1������ֱ��RQ��б��Ϊ-
��Q(x2��-
x2)
��
��
=
+
��1����ͬ��
=
+
��2��
�ɡ�PSQΪ�������Σ���
|OP|=|OQ|����3|OP|2=|OQ|2
����3[x12+(kx1)2]=x22+(
)2�������
=
��
3k2(
+
)=
+
����k2=-
��0��
���ԡ�OPQ�����������Σ�
|
| 3 |
����ķ���Ϊ
| x2 |
| 4 |
��2��ֱ�߷���Ϊy=
| 3 |
| 3 |
������Բ���̵�13x2-24
| 3 |
|
���ҳ���ʽ���AB=
| 16 |
| 13 |
��3����P��y���ϣ�Q��x����ʱ����PSQ�����������Σ�
��P����y����ʱ����ֱ��PS��б��Ϊk��P��x1��kx1������ֱ��RQ��б��Ϊ-
| 1 |
| k |
| 1 |
| k |
��
|
| 1 |
| x12 |
| 1 |
| 4 |
| k2 |
| 2 |
| 1 |
| x22 |
| 1 |
| 4 |
| 1 |
| 2k2 |
�ɡ�PSQΪ�������Σ���
| 3 |
����3[x12+(kx1)2]=x22+(
| x2 |
| k |
| 3k2 |
| x22 |
| 1 |
| x12 |
3k2(
| 1 |
| 4 |
| 1 |
| 2k2 |
| 1 |
| 4 |
| k2 |
| 2 |
| 5 |
| 4 |
���ԡ�OPQ�����������Σ�
������������Ҫ��������Բ���ʵ�Ӧ�ã��ҳ���ʽ��Ӧ�ã��Լ�Τ�ﶨ���ڽ��ֱ����Բ����λ�ù�ϵ�ж��е�Ӧ��

��ϰ��ϵ�д�
�����Ŀ