题目内容
11.已知f(x)=sinx-$\frac{1}{2}$x(x$∈[0,\frac{π}{2}]$,则f(x)的值域为( )| A. | [0,$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$] | B. | [1-$\frac{π}{4}$,$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$] | C. | [0,$\frac{1}{2}$-$\frac{π}{12}$] | D. | [1-$\frac{π}{4}$,$\frac{1}{2}$-$\frac{π}{12}$] |
分析 利用利用导数研究闭区间上的函数的单调性极值与最值即可得出.
解答 解:f(x)=sinx-$\frac{1}{2}$x(x$∈[0,\frac{π}{2}]$,
f′(x)=cosx-$\frac{1}{2}$,
则当$0≤x<\frac{π}{3}$时,f′(x)>0,此时函数f(x)单调递增;当$\frac{π}{3}<x≤\frac{π}{2}$时,f′(x)<0,此时函数f(x)单调递减.
∴当x=$\frac{π}{3}$时,函数f(x)取得最大值,$f(\frac{π}{3})$=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
而f(0)=0,f($\frac{π}{2}$)=1-$\frac{π}{4}$.
∴f(x)的值域为$[0,\frac{\sqrt{3}}{2}-\frac{π}{6}]$.
故选:A.
点评 本题考查了利用导数研究闭区间上的函数的单调性极值与最值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.下面几个空间图形中,虚线、实线使用不正确的有( )
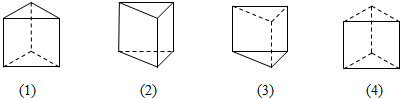

| A. | (2)(3) | B. | (1)(3) | C. | (3)(4) | D. | (4) |
16.设i是虚数单位,则复数z=$\frac{5}{i(i+2)}$的虚部为( )
| A. | -2 | B. | 2 | C. | -1 | D. | -2i |
3.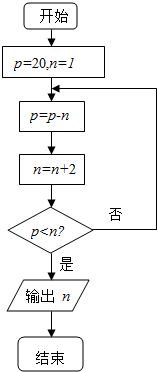 如图是一个程序框图,则输出的n的值是( )
如图是一个程序框图,则输出的n的值是( )
 如图是一个程序框图,则输出的n的值是( )
如图是一个程序框图,则输出的n的值是( )| A. | 3 | B. | 5 | C. | 7 | D. | 9 |