题目内容
【题目】已知公比为负值的等比数列{an}中，a1a5=4，a4=﹣1．
（1）求数列{an}的通项公式；
（2）设bn= 
+ 
+…+ 
，求数列{an+bn}的前n项和Sn ．
【答案】
（1）解：设等比数列{an}的公比为q＜0，
∵a1a5=4，a4=﹣1．
∴ 
， 
=﹣1，解得q=﹣ 
，a1=8．
∴ 
= 
（2）解：∵bn= 
+ 
+…+ 
=（n+1）[ 
+…+ 
]
=（n+1）× 
=n，
∴an+bn= +n，
其前n项和Sn=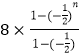 
+ 
= 
+
【解析】（1）设等比数列{an}的公比为q＜0，由a1a5=4，a4=﹣1．可得 ， =﹣1，解得即可；（2）由bn= + +…+ =（n+1）[ +…+ ]=n，可得an+bn= +n，再利用等差数列与等比数列的前n项和公式即可得出．
【考点精析】认真审题，首先需要了解等比数列的通项公式（及其变式）(通项公式：
)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系
)的相关知识才是答题的关键．
【题目】如图，矩形
中， 
， 
为边
的中点，将
沿直线
翻转成
.若
为线段
的中点，则在
翻折过程中：
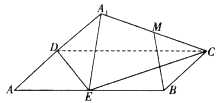
①
是定值；②点
在某个球面上运动；
③存在某个位置，使
；④存在某个位置，使
平面
.
其中正确的命题是_________.
【题目】某同学用“随机模拟方法”计算曲线
与直线
， 
所围成的曲边三角形的面积时，用计算机分别产生了10个在区间
上的均匀随机数
和10个区间
上的均匀随机数
（
， 
），其数据如下表的前两行.
| 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得这个曲边三角形面积的一个近似值是（ ）
A. 
B. 
C. 
D. 
