题目内容
如图1,在△ABC中,BC=3,AC=6,∠C=90°,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2。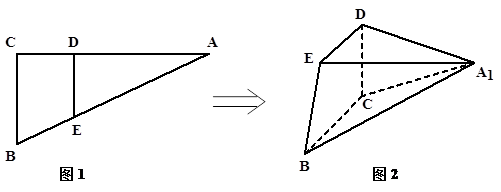
(1)求证:BC⊥平面A1DC;
(2)若CD=2,求BE与平面A1BC所成角的正弦值。
(1)详见解析;(2)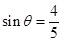
解析试题分析:(1)可以利用线线BC ,
,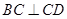 垂直,来证明线面BC⊥平面A1DC垂直;
垂直,来证明线面BC⊥平面A1DC垂直;
(2)可以以D为原点,分别以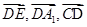 为x,y,z轴的正方向,建立空间直角坐标系,然后利用空间向量的线面角公式
为x,y,z轴的正方向,建立空间直角坐标系,然后利用空间向量的线面角公式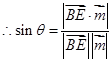 即可.
即可.
试题解析:(Ⅰ)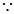 DE
DE ,DE//BC,
,DE//BC,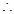 BC
BC 2分
2分
又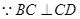 ,AD
,AD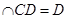
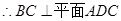 4分
4分
(2)以D为原点,分别以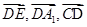 为x,y,z轴的正方向,
为x,y,z轴的正方向,
建立空间直角坐标系D-xyz 5分
说明:建系方法不唯一 ,不管左手系、右手系只要合理即可
在直角梯形CDEB中,过E作EF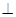 BC,EF=2,BF=1,BC=3 6分
BC,EF=2,BF=1,BC=3 6分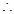 B(3,0,-2)E(2,0,0)C(0,0,-2)A1(0,4,0) 8分
B(3,0,-2)E(2,0,0)C(0,0,-2)A1(0,4,0) 8分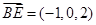
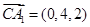
 9分
9分
设平面A1BC的法向量为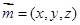
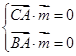

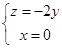 令y=1,
令y=1,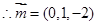 10分
10分
设BE与平面A1BC所成角为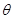 ,
,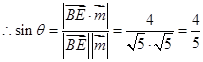 12分
12分
考点:(1)空间位置关系的证明;(2)利用向量解决立体几何问题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
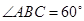 ,平面
,平面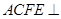 平面ABCD,四边形ACFE是矩形,AE=a.
平面ABCD,四边形ACFE是矩形,AE=a.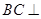 平面ACFE;
平面ACFE;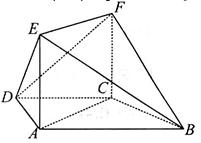
 中,
中,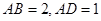 ,
,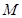 为
为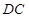 的中点.将
的中点.将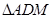 沿
沿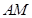 折起,使得平面
折起,使得平面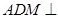 平面
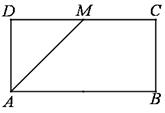
平面 .
.

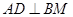 ;
;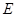 是线段
是线段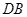 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角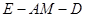 的余弦值为
的余弦值为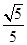 .
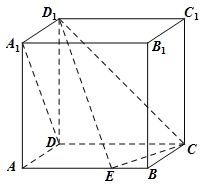
.
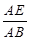 的值;
的值; 中,
中,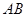 //
//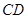 ,
,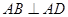 ,
,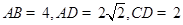 ,
,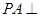 平面
平面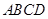 ,
,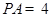 .
. 
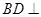 平面
平面 ;
;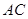 与
与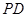 所成角的余弦值;
所成角的余弦值;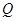 为线段
为线段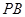 上一点,且直线
上一点,且直线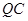 与平面
与平面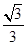 ,求
,求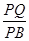 的值.
的值.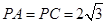 ,
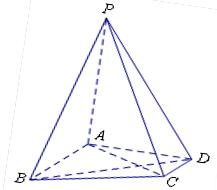
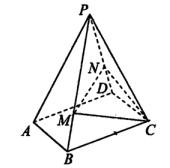
,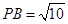 ,M、N两点分别在侧棱PB、PD上,
,M、N两点分别在侧棱PB、PD上,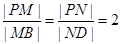 .
.
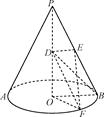
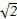 ,☉O的直径AB=2,C是
,☉O的直径AB=2,C是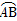 的中点,D为AC的中点.
的中点,D为AC的中点.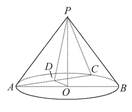
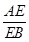 =
=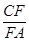 =
=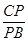 =
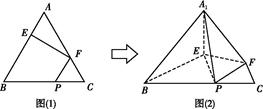
= (如图(1)),将△AEF沿EF折起到△
(如图(1)),将△AEF沿EF折起到△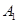 EF的位置,使二面角
EF的位置,使二面角 EF
EF