题目内容
 如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AD=1,AB=2,CD=3,F为AB中点,且EF∥AD.将梯形沿EF折起,使得平面ADEF⊥平面BCEF.
如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AD=1,AB=2,CD=3,F为AB中点,且EF∥AD.将梯形沿EF折起,使得平面ADEF⊥平面BCEF.(Ⅰ)求证:BC⊥平面BDE;
(Ⅱ)求CE与平面BCD所成角的正弦值.
【答案】分析:(Ⅰ)由题意可得DE⊥平面BCEF,进而可得BC⊥DE.结合BC⊥BE,由线面垂直的判定可得答案;
(Ⅱ)过E点作取EH⊥BD于H,连结HC.可证∠ECH是CE与平面BCD所成的角.在三角形中有已知数据可得其正弦值.
解答:证明:(Ⅰ)∵DE⊥EF,平面ADEF⊥平面BCEF,∴DE⊥平面BCEF,∴BC⊥DE.
由F为AB中点,可得BC⊥BE,又∵DE∩BE=E,
∴BC⊥平面BDE.
(Ⅱ)过E点作取EH⊥BD于H,连结HC.
∵BC⊥平面BDE,∴平面BDE⊥平面BCD,∴EH⊥平面BCD,
∴∠ECH是CE与平面BCD所成的角.
由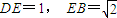 ,得
,得 ,
,
∴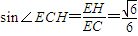 .
.
∴CE与平面BCD所成角的正弦值为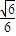 .
.
点评:本题考查直线与平面垂直的判定,以及直线与平面所成的角,属中档题.
(Ⅱ)过E点作取EH⊥BD于H,连结HC.可证∠ECH是CE与平面BCD所成的角.在三角形中有已知数据可得其正弦值.
解答:证明:(Ⅰ)∵DE⊥EF,平面ADEF⊥平面BCEF,∴DE⊥平面BCEF,∴BC⊥DE.
由F为AB中点,可得BC⊥BE,又∵DE∩BE=E,

∴BC⊥平面BDE.
(Ⅱ)过E点作取EH⊥BD于H,连结HC.
∵BC⊥平面BDE,∴平面BDE⊥平面BCD,∴EH⊥平面BCD,
∴∠ECH是CE与平面BCD所成的角.
由
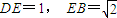 ,得
,得 ,
,∴
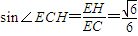 .
.∴CE与平面BCD所成角的正弦值为
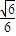 .
.点评:本题考查直线与平面垂直的判定,以及直线与平面所成的角,属中档题.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则