题目内容
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=| 2 |
(Ⅰ)求证:平面SAB⊥平面SAD;
(Ⅱ)设SB的中点为M,且DM⊥MC,试求出四棱锥S-ABCD的体积.
分析:(I)由已知中,∠A=∠D=90°SD⊥平面ABCD,我们易得AB⊥AD,SD⊥AB,由线面垂直的判定定理,可得AB⊥平面SAD,再由面面垂直的判定定理,可得平面SAB⊥平面SAD;
(II)连接BD,∵∠A=∠D=90°,AB=AD=a,SD=
a,我们可得△DBA为等腰直角三角形,结合SB的中点为M,且DM⊥MC,我们易得四棱锥S-ABCD的高为SD,分别求出棱锥的底面面积和高,代入棱锥的体积公式,即可得到答案.
(II)连接BD,∵∠A=∠D=90°,AB=AD=a,SD=
| 2 |
解答:解: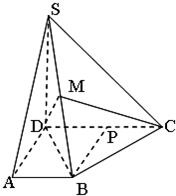 (Ⅰ)证明:∵∠A=90°,∴AB⊥AD
(Ⅰ)证明:∵∠A=90°,∴AB⊥AD
又SD⊥平面ABCD,AB?平面ABCD,
∴SD⊥AB
∴AB⊥平面SAD.
又AB?平面SAB,
∴平面SAB⊥平面SAD.
(Ⅱ)连接BD,∵∠A=∠D=90°,AB=AD=a,
∴BD=
a=SD
∴∠DBA=45°
又M为SB中点,
∴DM⊥SB
由条件DM⊥MC,MC∩SB=M,∴DM⊥面SBC,又BC?面SBC,
则DM⊥BC,由(1)可知SD⊥BC,SD∩DM=D,∴BC⊥面SDB,则BC⊥BD,
由平面几何知识,则△BDC是等腰直角三角形,
则DC=
DB=2a,
故VS-ABCD=
SABCD•SD=
(
)•a.
•a=
a3
 (Ⅰ)证明:∵∠A=90°,∴AB⊥AD
(Ⅰ)证明:∵∠A=90°,∴AB⊥AD又SD⊥平面ABCD,AB?平面ABCD,
∴SD⊥AB
∴AB⊥平面SAD.
又AB?平面SAB,
∴平面SAB⊥平面SAD.
(Ⅱ)连接BD,∵∠A=∠D=90°,AB=AD=a,
∴BD=
| 2 |
∴∠DBA=45°
又M为SB中点,
∴DM⊥SB
由条件DM⊥MC,MC∩SB=M,∴DM⊥面SBC,又BC?面SBC,
则DM⊥BC,由(1)可知SD⊥BC,SD∩DM=D,∴BC⊥面SDB,则BC⊥BD,
由平面几何知识,则△BDC是等腰直角三角形,
则DC=
| 2 |
故VS-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| a+2a |
| 2 |
| 2 |
| ||
| 2 |
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的体积,熟练掌握空间直线与直线、直线与平面、平面与平面位置关系的判定、性质、定义、几何特征是解答此类问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则