题目内容
（本小题共12分） 设数列
的前
项和为
，已知
， 
（
）.（Ⅰ）求证：数列
为等差数列，并分别写出
和
关于的表达式；（Ⅱ）若
，
为数列
前
项和，求
；（Ⅲ）是否存在自然数，使得
? 若存在，求的值；若不存在，说明理由.
(Ⅰ) 
(Ⅱ) 
. （Ⅲ）
解析:
：（Ⅰ）当
时，
，
得
. ∴数列
是以
为首项，4为公差的等差数列.
∴
.
（Ⅱ）
=
=
=
=
=.
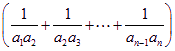
（Ⅲ）由得： 
，
∴
.
令
，得，所以，存在满足条件的自然数.
练习册系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
的焦点坐
标为
（
），点M（
，
）在椭圆E上
（1）求椭圆E的方程；（2）O为坐标原点，⊙
的任意一条切线与椭圆E有两个交点
，
且
，求⊙
⊥平面
，
∥
是正三角形，
，且
是
的中点
∥平面
；
．
名，女同学有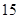
名，老师按照分层抽样的方法组建了一个
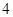人的课外兴趣小组．
名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
，
，求证：
.
的值.