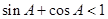题目内容
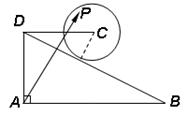
如图,在直角梯形 中,
中,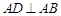 ,
,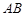 ∥
∥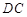 ,
,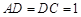 ,
,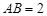 ,动点
,动点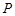 在以点
在以点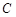 为圆心,且与直线
为圆心,且与直线 相切的圆上或圆内移动,设
相切的圆上或圆内移动,设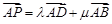 (
(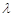 ,
,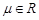 ),则
),则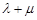 取值范围是
取值范围是
 中,
中,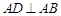 ,
,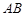 ∥
∥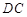 ,
,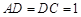 ,
,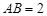 ,动点
,动点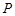 在以点
在以点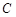 为圆心,且与直线
为圆心,且与直线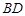 相切的圆上或圆内移动,设
相切的圆上或圆内移动,设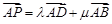 (
(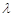 ,
,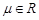 ),则
),则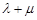 取值范围是
取值范围是
A.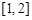 | B.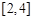 | C.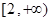 | D.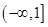 |
A
建立以C为原点,DC为X轴的平面直角坐标系
则向量AD=(0,1) AB=(2,0)圆C的方程:x²+y²=R²
∵DC∥AB,所以∠CDB=∠ABD,所以直角△ADB∽直角△QCD(Q为圆与BD的切点)
所以QC/AD=CD/BD ∴QC=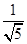 =R
=R
设P(x,y) 因为P在圆上或园内,∴其坐标满足:x²+y²≤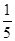
向量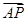 =(x+1,y+1)=
=(x+1,y+1)=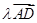 +
+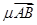 =(
=(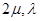 )
)
从而: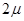 ="x+1,"
="x+1," 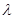 =y+1 ∴ (
=y+1 ∴ (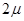 -1)²+(
-1)²+(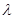 -1)²≤
-1)²≤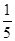
可以推断,当P在圆上时,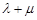 达到最大值, 此时:(
达到最大值, 此时:(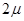 -1)²+(
-1)²+(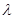 -1)²=
-1)²=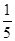
设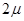 -1=
-1=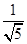 cosA,
cosA,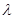 -1=
-1=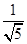 sinA 所以
sinA 所以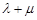 =
=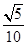 (cosA+2sinA)+
(cosA+2sinA)+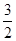
由于cosA+2sinA=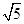 sin(A+B) 所以最大值取
sin(A+B) 所以最大值取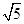 ,所以
,所以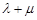 的最大值为
的最大值为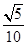 X
X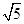 +
+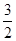 =2
=2
赞同
最小值为1.
则向量AD=(0,1) AB=(2,0)圆C的方程:x²+y²=R²
∵DC∥AB,所以∠CDB=∠ABD,所以直角△ADB∽直角△QCD(Q为圆与BD的切点)
所以QC/AD=CD/BD ∴QC=
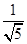 =R
=R设P(x,y) 因为P在圆上或园内,∴其坐标满足:x²+y²≤
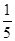
向量
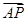 =(x+1,y+1)=
=(x+1,y+1)=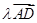 +
+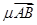 =(
=(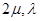 )
)从而:
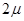 ="x+1,"
="x+1," 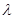 =y+1 ∴ (
=y+1 ∴ (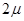 -1)²+(
-1)²+(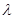 -1)²≤
-1)²≤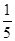
可以推断,当P在圆上时,
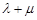 达到最大值, 此时:(
达到最大值, 此时:(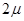 -1)²+(
-1)²+(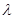 -1)²=
-1)²=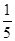
设
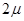 -1=
-1=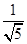 cosA,
cosA,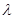 -1=
-1=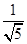 sinA 所以
sinA 所以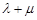 =
=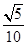 (cosA+2sinA)+
(cosA+2sinA)+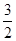
由于cosA+2sinA=
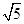 sin(A+B) 所以最大值取
sin(A+B) 所以最大值取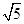 ,所以
,所以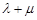 的最大值为
的最大值为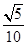 X
X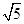 +
+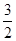 =2
=2赞同
最小值为1.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
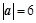 ,
,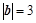 ,
, ,则向量
,则向量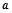 在向量
在向量 方向上的投影是( )
方向上的投影是( )
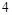
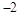
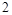
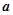 =
=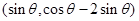 ,
,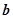 =
= .
.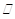
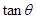 的值;
的值; 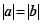 ,
,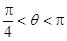 ,求
,求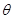 的值.
的值.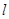 上存在不同的三个点
上存在不同的三个点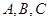 ,使得关于实数
,使得关于实数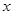 的方程
的方程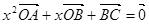 有解(点O不在
有解(点O不在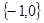
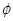
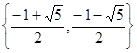
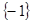
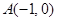 ,
,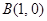 ,动点
,动点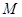 的轨迹曲线
的轨迹曲线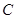 满足
满足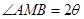 ,
,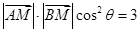 ,过点
,过点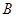 的直线交曲线
的直线交曲线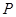 、
、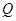 两点.
两点.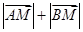 的值,并写出曲线
的值,并写出曲线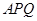 面积的最大值.
面积的最大值.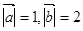 ,
,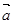 与
与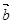 的夹角为
的夹角为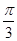 ,那么
,那么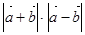 =
= 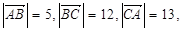 则
则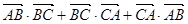 的值等于 .
的值等于 . 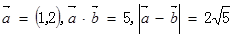 ,则
,则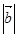 等于 ( )
等于 ( )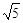
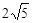
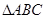 分别满足下列条件,
分别满足下列条件,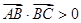 ; (2)
; (2)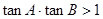 ;
;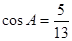 ,
,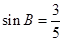 ; (4)
; (4)