题目内容
(本小题满分12分)
已知点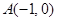 ,
,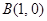 ,动点
,动点 的轨迹曲线
的轨迹曲线 满足
满足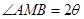 ,
,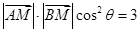 ,过点
,过点 的直线交曲线
的直线交曲线 于
于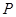 、
、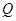 两点.
两点.
(1)求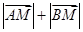 的值,并写出曲线
的值,并写出曲线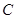 的方程;
的方程;
(2)求△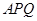 面积的最大值.
面积的最大值.
已知点
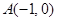 ,
,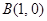 ,动点
,动点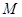 的轨迹曲线
的轨迹曲线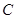 满足
满足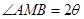 ,
,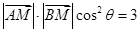 ,过点
,过点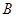 的直线交曲线
的直线交曲线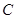 于
于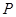 、
、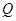 两点.
两点.(1)求
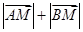 的值,并写出曲线
的值,并写出曲线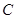 的方程;
的方程;(2)求△
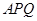 面积的最大值.
面积的最大值.解:(1)设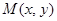 ,在△
,在△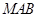 中,
中,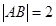 ,
,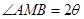 ,根据余弦定理得
,根据余弦定理得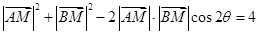 . (2分)
. (2分)
即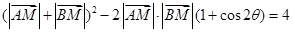 .
.
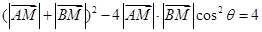 .
.
而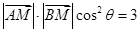 ,所以
,所以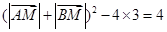 .
.
所以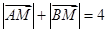 . (4分)
. (4分)
又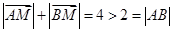 ,
,
因此点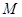 的轨迹是以
的轨迹是以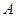 、
、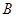 为焦点的椭圆(点
为焦点的椭圆(点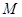 在
在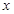 轴上也符合题意),
轴上也符合题意),
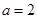 ,
,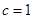 .
.
所以曲线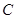 的方程为
的方程为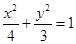 . (6分)
. (6分)
(2)设直线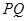 的方程为
的方程为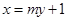 .
.
由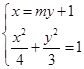 ,消去x并整理得
,消去x并整理得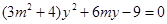 . ①
. ①
显然方程①的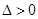 ,设
,设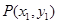 ,
,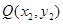 ,则
,则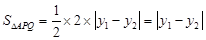
由韦达定理得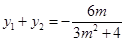 ,
,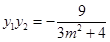 . (9分)
. (9分)
所以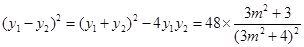 .
.
令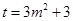 ,则
,则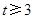 ,
,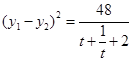 .
.
由于函数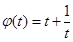 在
在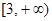 上是增函数.
上是增函数.
所以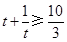 ,当
,当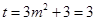 ,即
,即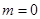 时取等号.
时取等号.
所以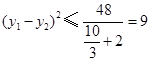 ,即
,即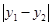 的最大值为3.
的最大值为3.
所以△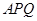 面积的最大值为3,此时直线
面积的最大值为3,此时直线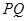 的方程为
的方程为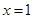 . (12分)
. (12分)
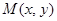 ,在△
,在△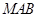 中,
中,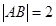 ,
,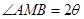 ,根据余弦定理得
,根据余弦定理得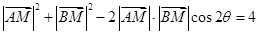 . (2分)
. (2分)即
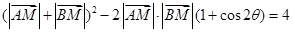 .
.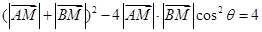 .
.而
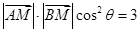 ,所以
,所以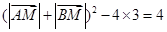 .
. 所以
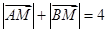 . (4分)
. (4分) 又
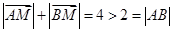 ,
,因此点
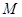 的轨迹是以
的轨迹是以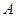 、
、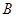 为焦点的椭圆(点
为焦点的椭圆(点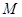 在
在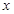 轴上也符合题意),
轴上也符合题意),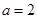 ,
,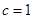 .
.所以曲线
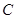 的方程为
的方程为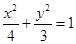 . (6分)
. (6分)(2)设直线
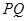 的方程为
的方程为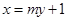 .
.由
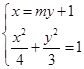 ,消去x并整理得
,消去x并整理得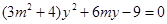 . ①
. ①显然方程①的
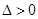 ,设
,设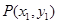 ,
,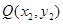 ,则
,则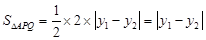
由韦达定理得
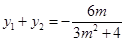 ,
,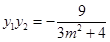 . (9分)
. (9分)所以
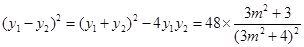 .
.令
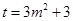 ,则
,则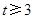 ,
,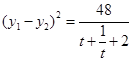 .
.由于函数
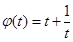 在
在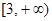 上是增函数.
上是增函数.所以
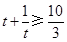 ,当
,当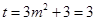 ,即
,即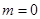 时取等号.
时取等号.所以
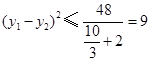 ,即
,即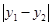 的最大值为3.
的最大值为3.所以△
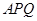 面积的最大值为3,此时直线
面积的最大值为3,此时直线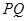 的方程为
的方程为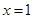 . (12分)
. (12分)略

练习册系列答案
相关题目
 中,
中,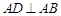 ,
,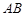 ∥
∥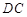 ,
,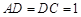 ,
,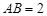 ,动点
,动点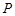 在以点
在以点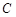 为圆心,且与直线
为圆心,且与直线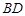 相切的圆上或圆内移动,设
相切的圆上或圆内移动,设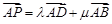 (
(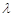 ,
,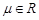 ),则
),则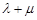 取值范围是
取值范围是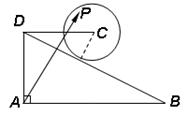
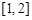
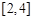
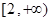
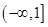
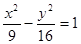 的左、右焦点分别为F1、F2,P为双曲线C的右支上一点,且|PF2|=|F1F2|,则ΔPF1F2的面积等于( )
的左、右焦点分别为F1、F2,P为双曲线C的右支上一点,且|PF2|=|F1F2|,则ΔPF1F2的面积等于( )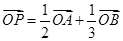 ,则
,则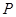 、
、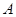 、
、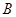 三点共线;
三点共线; 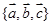 为空间的一个基底,则
为空间的一个基底,则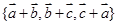 构成空间的另一个基底;
构成空间的另一个基底;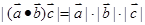 ;
; 为直角三角形的充要条件是
为直角三角形的充要条件是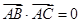 .
.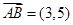 ,
,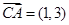 则
则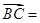 ( )
( )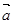 与
与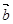 的夹角为120°,且
的夹角为120°,且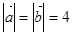 ,那么
,那么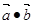 的值为
的值为  =
=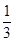
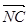 ,P是BN上的一点,若
,P是BN上的一点,若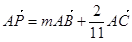 ,则实数的值为__________
,则实数的值为__________ 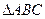 中,E.F分别为边AB.AC上的点,且
中,E.F分别为边AB.AC上的点,且 ,若
,若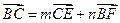 ,则
,则