题目内容
(本小题满分14分)
设数列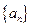 的前
的前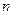 项和为
项和为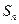 ,对任意的正整数
,对任意的正整数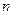 ,都有
,都有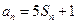 成立,记
成立,记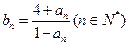 。
。
(Ⅰ)求数列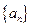 与数列
与数列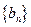 的通项公式;
的通项公式;
(Ⅱ)设数列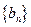 的前
的前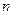 项和为
项和为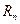 ,是否存在正整数
,是否存在正整数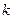 ,使得
,使得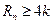 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数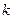 ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅲ)记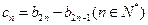 ,设数列
,设数列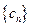 的前
的前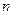 项和为
项和为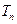 ,求证:对任意正整数
,求证:对任意正整数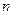 都有
都有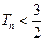 。
。
设数列
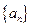 的前
的前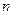 项和为
项和为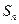 ,对任意的正整数
,对任意的正整数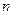 ,都有
,都有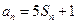 成立,记
成立,记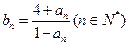 。
。(Ⅰ)求数列
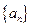 与数列
与数列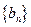 的通项公式;
的通项公式;(Ⅱ)设数列
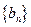 的前
的前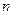 项和为
项和为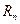 ,是否存在正整数
,是否存在正整数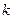 ,使得
,使得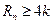 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数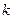 ;若不存在,请说明理由;
;若不存在,请说明理由;(Ⅲ)记
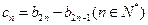 ,设数列
,设数列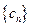 的前
的前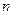 项和为
项和为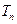 ,求证:对任意正整数
,求证:对任意正整数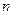 都有
都有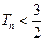 。
。(Ⅰ)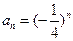 ,
,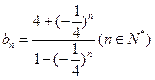
(Ⅱ)不存在正整数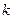 ,使得
,使得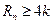 成立,理由见解析。
成立,理由见解析。
(Ⅲ)证明见解析。
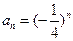 ,
,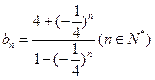
(Ⅱ)不存在正整数
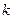 ,使得
,使得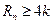 成立,理由见解析。
成立,理由见解析。(Ⅲ)证明见解析。
(Ⅰ)当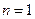 时,
时,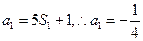
又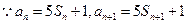
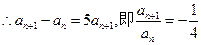
∴数列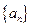 是首项为
是首项为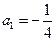 ,公比为
,公比为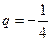 的等比数列,
的等比数列,
∴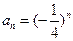 ,
,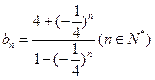 ……………………………3分
……………………………3分
(II)不存在正整数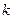 ,使得
,使得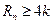 成立。
成立。
证明:由(I)知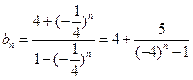
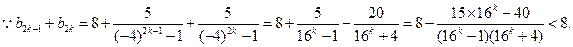
∴当n为偶数时,设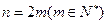
∴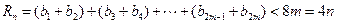
当n为奇数时,设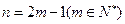
∴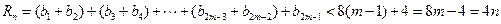
∴对于一切的正整数n,都有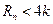
∴不存在正整数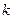 ,使得
,使得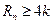 成立。………………………………8分
成立。………………………………8分
(III)由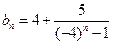 得
得
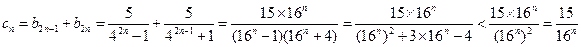 又
又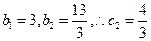 ,
,
当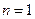 时,
时,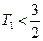 ,
,
当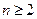 时,
时,
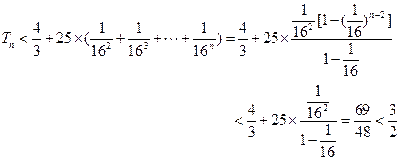 …………………14分
…………………14分
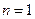 时,
时,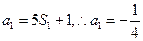
又
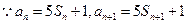
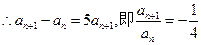
∴数列
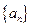 是首项为
是首项为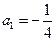 ,公比为
,公比为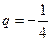 的等比数列,
的等比数列,∴
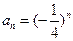 ,
,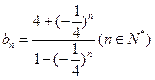 ……………………………3分
……………………………3分(II)不存在正整数
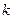 ,使得
,使得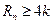 成立。
成立。证明:由(I)知
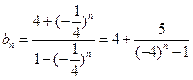
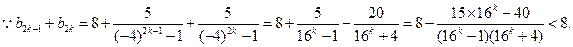
∴当n为偶数时,设
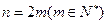
∴
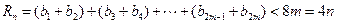
当n为奇数时,设
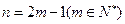
∴
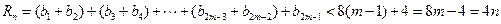
∴对于一切的正整数n,都有
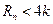
∴不存在正整数
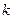 ,使得
,使得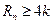 成立。………………………………8分
成立。………………………………8分(III)由
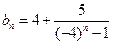 得
得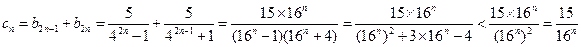 又
又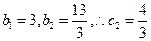 ,
,当
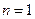 时,
时,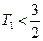 ,
,当
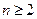 时,
时,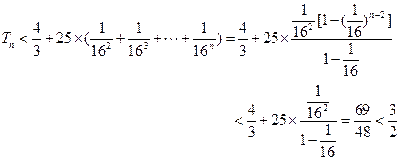 …………………14分
…………………14分
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 中,
中,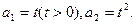 当
当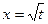 时,函数
时,函数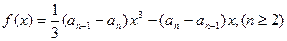 取得极值。
取得极值。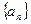 的通项公式。(6分)
的通项公式。(6分)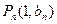 。过函数
。过函数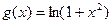 图象上的点
图象上的点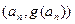 的切线始终与
的切线始终与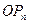 平行(O是坐标原点)。求证:当
平行(O是坐标原点)。求证:当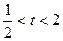 时,不等式
时,不等式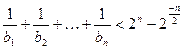 对任意
对任意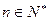
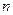 ≥2,用
≥2,用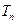 表示关于
表示关于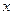 的一元二次方程
的一元二次方程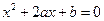 有实数根的有序数组
有实数根的有序数组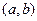 的组数,其中
的组数,其中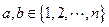 (
(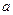 和
和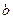 可以相等);对于随机选取的
可以相等);对于随机选取的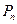 为关于
为关于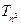 和
和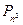 ;
;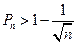 。
。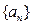 中,
中,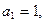 点
点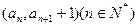 在函数
在函数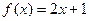 的图像上,
的图像上,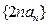 的前n项和
的前n项和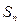 .
. 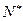 上的函数
上的函数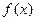 满足
满足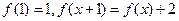 ,则
,则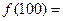 .
.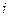 行共有
行共有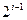 个正整数.设
个正整数.设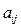 (i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数.
(i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数. 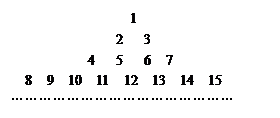
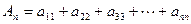
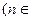 N*),试比较
N*),试比较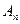 与
与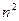
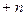 的大小,并说明理由.
的大小,并说明理由.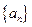 为等差数列,首项
为等差数列,首项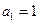 ,公差
,公差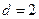 ,
,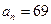 ,则
,则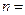 ( )
( ) ______________.
______________. 是等差数列{
是等差数列{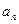 }的前n项和,
}的前n项和,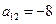 ,
, 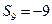 ,则
,则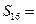 。
。