题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
在数列 中,
中,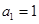 ,
, .
.
(1)设
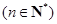 ,证明:数列
,证明:数列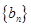 是等差数列;
是等差数列;
(2)设数列 的前
的前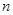 项和为
项和为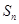 ,求
,求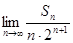 的值;
的值;
(3)设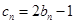 ,数列
,数列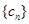 的前
的前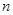 项和为
项和为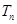 ,
,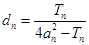 ,是否存在实数
,是否存在实数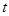 ,使得对任意的正整数
,使得对任意的正整数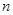 和实数
和实数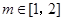 ,都有
,都有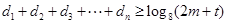 成立?请说明理由.
成立?请说明理由.
【答案】
略
【解析】(1)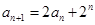 ,
,  ,
(2分)
,
(2分)
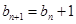 ,
故
,
故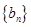 为等差数列,
为等差数列,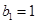 ,
,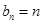 .
(4分)
.
(4分)
(2)由(1)可得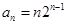 (6分)
(6分)
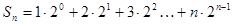
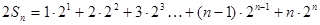
两式相减,得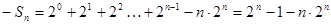 ,即
,即
 (8分)
(8分) 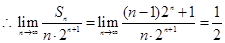 (10分)
(10分)
(3)由(1)可得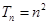 ,(12分) ∴
,(12分) ∴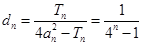 ,
,

∴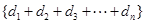 单调递增,即
单调递增,即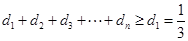 , (14分)要使
, (14分)要使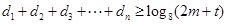 对任意正整数
对任意正整数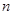 成立,
成立,
必须且只需 ,即
,即 对任意
对任意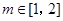 恒成立. (16分)∴
恒成立. (16分)∴ ,即
,即  矛盾.
矛盾.
∴满足条件的实数 不存在. (18分)
不存在. (18分)

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处