题目内容
【题目】某班有男生27名，女生18名，用分层抽样的方法从该班中抽取5名学生去敬老院参加献爱心活动.
（1）求从该班男生、女生中分别抽取的人数；
（2）为协助敬老院做好卫生清扫工作，从参加活动的5名学生中随机抽取2名，求这2名学生均为女生的概率.
【答案】（1）从该班男生、女生中抽取的人数分别为3，2（2）
【解析】
（1）根据分层抽样的基本原则可计算求得结果；
（2）列举出随机抽取
名学生的所有基本事件，从中找到名学生均为女生的基本事件个数，根据古典概型概率公式可求得结果.
（1）设从该班男生、女生中抽取的人数分别为
，则
，
从该班男生、女生中抽取的人数分别为
，
（2）记参加活动的名男生分别为
，名女生分别为
则随机抽取名学生的所有基本事件为：
，共
个
记“名学生均为女生”为事件
，则事件包含的基本事件只有
个：
练习册系列答案
相关题目
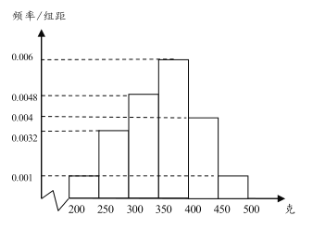
【题目】某机构对某市工薪阶层的收入情况与超前消费行为进行调查，随机抽查了200人，将他们的月收入（单位：百元）频数分布及超前消费的认同人数整理得到如下表格：
月收入（百元） |
|
|
|
|
|
|
频数 | 20 | 40 | 60 | 40 | 20 | 20 |
认同超前消费的人数 | 8 | 16 | 28 | 21 | 13 | 16 |
（1）根据以上统计数据填写下面
列联表，并回答是否有99%的把握认为当月收入以8000元为分界点时，该市的工薪阶层对“超前消费”的态度有差异；
月收入不低于8000元 | 月收入低于8000元 | 总计 | |
认同 | |||
不认同 | |||
总计 |
（2）若从月收入在
的被调查对象中随机选取2人进行调查，求至少有1个人不认同“超前消费”的概率.
参考公式：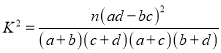
（其中
）.
附表：
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
