题目内容
把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,试就方程组(1)求方程组只有一解的概率;
(2)求方程组只有正数解的概率.
思路解析:注意通过对方程的解所满足的限制条件,确定将骰子投掷两次每次出现的点数来列举出事件所包含的基本事件的总数.
解:掷骰子第一次出现的点数为a共有6种情况,第二次出现的点数为b也有6种情况,故基本事件的总数n=6×6=36种.
(1)方程组![]() 只有一解的等价条件是:
只有一解的等价条件是:![]() ≠
≠![]() 即b≠2a,故符合条件基本事件为总的基本事件中除去(1,2)、(2,4)、(3,6)三种,即事件A“方程组只有一解”所包含的基本事件总数m=33.根据古典概型可知P(A)=
即b≠2a,故符合条件基本事件为总的基本事件中除去(1,2)、(2,4)、(3,6)三种,即事件A“方程组只有一解”所包含的基本事件总数m=33.根据古典概型可知P(A)=![]() .
.
(2)由方程组![]() 得
得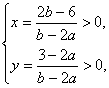 >0,故当b>2a时,有
>0,故当b>2a时,有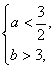 符合条件的基本事件有(1,4)、(1,5)、(1,6);当b<2a,
符合条件的基本事件有(1,4)、(1,5)、(1,6);当b<2a,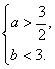 符合条件的基本事件有(2,1)、(2,2)、(3,1)、(3,2)、(4,1)、(4,2)、(5,1)、(5,2)、(6,1)、(6,2).故事件B“方程组只有正数解”包含的基本事件总数m=13,
符合条件的基本事件有(2,1)、(2,2)、(3,1)、(3,2)、(4,1)、(4,2)、(5,1)、(5,2)、(6,1)、(6,2).故事件B“方程组只有正数解”包含的基本事件总数m=13,
故P(A)=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(文)把一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b.已知直线l1:x+2y=2,直线l2:ax+by=4,则两直线l1、l2平行的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|