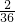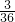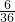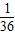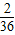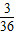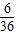题目内容
(文)把一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b.已知直线l1:x+2y=2,直线l2:ax+by=4,则两直线l1、l2平行的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:把一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,则不同的结果数是36种,直线l1:x+2y=2,直线l2:ax+by=4,则两直线l1、l2平行的情况为b=2a,且a≠2,的出符合条件的所有基本事件数,由公式计算出概率,选出正确选项
解答:解:把一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,则不同的结果数是36种,
使得直线l1:x+2y=2,直线l2:ax+by=4,两直线l1、l2平行的情况有a=1,b=2;a=3,b=6,共两种
故两直线l1、l2平行的概率为
=
故选B
使得直线l1:x+2y=2,直线l2:ax+by=4,两直线l1、l2平行的情况有a=1,b=2;a=3,b=6,共两种
故两直线l1、l2平行的概率为
| 2 |
| 36 |
| 1 |
| 18 |
故选B
点评:本题考查古典概率模型及其计算公式,解本题的关键是理解事件“直线l1:x+2y=2,直线l2:ax+by=4,则两直线l1、l2平行”求出此事件包含的基本事件数,熟练掌握公式也很关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目