题目内容
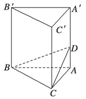
如图所示,正三棱柱![]() 的底面边长是2,侧棱长是,D是AC的中点。
的底面边长是2,侧棱长是,D是AC的中点。
 (1)求证:
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直线![]() 与平面
与平面![]() 所成的角的正弦值。
所成的角的正弦值。
解法一:(1)设![]() 与
与![]() 相交于点P,连接PD,则P为
相交于点P,连接PD,则P为![]() 中点,
中点,

![]() D为AC中点,
D为AC中点,![]() PD//
PD//![]() .
.
又![]() PD
PD![]() 平面
平面![]() D,
D,![]()
![]() //平面
//平面![]() D
D
(2)![]() 正三棱住
正三棱住![]() ,
,![]()
![]()
![]() 底面ABC。
底面ABC。
又![]() BD
BD![]() AC
AC![]()
![]()
![]() BD
BD
![]()
![]() 就是二面角
就是二面角![]() 的平面角。
的平面角。
![]()
![]() =
=![]() ,AD=
,AD=![]() AC=1
AC=1![]() tan
tan ![]() =
=![]()
![]()
![]() =
=![]() , 即二面角
, 即二面角![]() 的大小是
的大小是![]()
(3)由(2)作AM![]()
![]() ,M为垂足。
,M为垂足。
![]() BD
BD![]() AC,平面
AC,平面![]()
![]() 平面ABC,平面
平面ABC,平面![]()
![]() 平面ABC=AC
平面ABC=AC
![]() BD
BD![]() 平面
平面![]() ,
,![]() AM
AM![]() 平面
平面![]() ,
,![]() BD
BD![]() AM
AM
![]()
![]()
![]() BD = D
BD = D![]() AM
AM![]() 平面
平面![]() ,连接MP,则
,连接MP,则![]() 就是直线
就是直线![]() 与平面
与平面![]() D所成的角。
D所成的角。
![]()
![]() =
=![]() ,AD=1,
,AD=1,![]() 在Rt
在Rt![]()
![]() D中,
D中,![]() =
=![]() ,
,
![]()
![]() ,
,![]() ,
,![]()

![]() 直线
直线![]() 与平面
与平面![]() D所成的角的正弦值为
D所成的角的正弦值为![]()
解法二:(1)同解法一(2)如图建立空间直角坐标系,
 则D(0,0,0),A(1,0,0),
则D(0,0,0),A(1,0,0),![]() (1,0,
(1,0,![]() ),B(0,
),B(0,![]() ,0),
,0),![]() (0,
(0,![]() ,
,![]() )
)
![]()
![]() =(-1,
=(-1,![]() ,-
,-![]() ),
),![]() =(-1,0,-
=(-1,0,-![]() )
)
设平面![]() 的法向量为n=(x,y,z)
的法向量为n=(x,y,z)
则n![]()
n![]()
则有 ,得n=(
,得n=(![]() ,0,1)
,0,1)
由题意,知![]() =(0,0,
=(0,0,![]() )是平面ABD的一个法向量。
)是平面ABD的一个法向量。
设n与![]() 所成角为
所成角为![]() ,则
,则 ,
,![]()
![]()
![]() 二面角
二面角![]() 的大小是
的大小是![]()
(3)由已知,得![]() =(-1,
=(-1,![]() ,
,![]() ),n=(
),n=(![]() ,0,1)则
,0,1)则
![]() 直线
直线![]() 与平面
与平面![]() D所成的角的正弦值为
D所成的角的正弦值为![]() .
.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目

 的底面边长与侧棱长均为
的底面边长与侧棱长均为 ,
, 为
为 中点.
中点. ∥平面
∥平面 ;
; 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
 ,D为BC上的一点,在截面ADC1中,∠ADC1=90°,求二面角C1-AD-C的大小。
,D为BC上的一点,在截面ADC1中,∠ADC1=90°,求二面角C1-AD-C的大小。