题目内容
在△ABC 中,sinA:sinB:sinC=3:2:4,则cosC的值为( )
A. | B.- | C. | D.- |
D
解析试题分析:∵sinA:sinB:sinC=3:2:4,∴a:b:c=3:2:4,设a=3k,则b=2k,c=4k,∴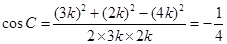 ,故选D
,故选D
考点:本题考查了余弦定理的运用
点评:熟练掌握余弦定理及其变形是解决此类问题的关键,属基础题

练习册系列答案
相关题目
在△ABC中,若 ,则△ABC是( )
,则△ABC是( )
| A.有一内角为30°的直角三角形 | B.等腰直角三角形 |
| C.有一内角为30°的等腰三角形 | D.等边三角形 |
△ABC中, a = 1, b = ,A=30°,则B等于 ( )
,A=30°,则B等于 ( )
| A.60° | B.60°或120° | C.30°或150° | D.120° |
在△ABC中,A=60°,a=,b=,则
| A.B=45°或135° | B.B=135° | C.B=45° | D.以上答案都不对 |
在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定 |
已知在△ABC中,sinA∶sinB∶sinC=3∶5∶7,那么这个三角形的最大角是 ( )
| A.135° | B.90° | C.120° | D.150 |
在△ABC中,a=3,b= ,c=2,那么B等于
,c=2,那么B等于
| A.30° | B.45° | C.60° | D.120° |
在 中,已知
中,已知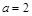 ,
, ,
, ,则
,则 的面积是( ).
的面积是( ).
A. | B. | C. | D. |
 ,则
,则 =( )
=( )  B.
B.  C.
C. D.
D.