题目内容
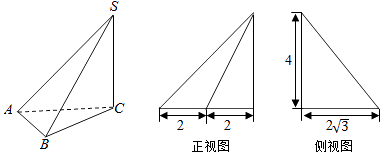
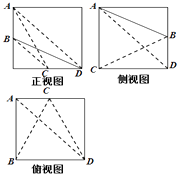
【题目】如图,已知四棱锥P﹣ABCD,侧面PAD是正三角形,底面ABCD是菱形,∠BAD=60°,设平面PAD∩平面PBC=l. 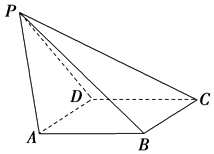
(Ⅰ)求证:l∥平面ABCD;
(Ⅱ)求证:PB⊥BC.
【答案】证明:(Ⅰ)∵BC平面PAD,AD平面PAD,AD∥BC,
∴BC∥平面PAD
又BC平面PBC,平面PAD∩平面PBC=l,
∴BC∥l.
又∵l平面ABCD,BC平面ABCD,
∴l∥平面ABCD.
(Ⅱ)取AD中点O,连OP、OB,

由已知得:OP⊥AD,OB⊥AD,
又∵OP∩OB=O,
∴AD⊥平面POB,
∵BC∥AD,
∴BC⊥平面POB,
∵PB平面POB,
∴BC⊥PB.
【解析】(Ⅰ)由已知利用线面平行的判定可证BC∥平面PAD,利用线面平行的性质可证BC∥l,进而利用线面平行的判定证明l∥平面ABCD.(Ⅱ)取AD中点O,连OP、OB,由已知得:OP⊥AD,OB⊥AD,利用线面垂直的判定可证AD⊥平面POB,由BC∥AD,可证BC⊥平面POB,利用线面垂直的性质即可证明BC⊥PB.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的性质的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行才能正确解答此题.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】某百货公司1~6月份的销售量x与利润y的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(参考公式: ![]() =
= 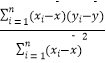 )=
)= 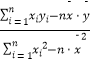 ,
, ![]() .
.
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程 ![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?