题目内容
16.(1)已知z1,z2是两个虚数,并且z1+z2与z1z2均为实数,求证:z1,z2是共轭复数(2)求证:无论θ为何值,方程x2-(tanθ+i)x-(i+2)=0都不可能有纯虚数根.
分析 (1)设z1=a+bi,z2=c+di(a,b,c,d∈R),且b,d≠0,则z1+z2=(a+c)+(b+d)i为实数,可得b+d=0.由z1z2=(ac-bd)+(ad+bc)i为实数,可得bc+ad=0,
把d=-b代入上式可得c=a.即可证明.
(2)假设此方程有纯虚数根bi(b∈R且b≠0),代入可得:(bi)2-(tanθ+i)bi-(i+2)=0,化为(b2-b+2)+(btanθ+1)i=0,由b2-b+2=0无实数根,可得设不成立,因此原命题成立.
解答 证明:(1)设z1=a+bi,z2=c+di(a,b,c,d∈R),且b,d≠0,
则z1+z2=(a+c)+(b+d)i为实数,可得b+d=0.
由z1z2=(ac-bd)+(ad+bc)i为实数,可得bc+ad=0,
把d=-b代入上式可得:b(c-a)=0,
∵b≠0,∴c=a.∴z1,z2是共轭复数.
(2)假设此方程有纯虚数根bi(b∈R且b≠0),代入可得:(bi)2-(tanθ+i)bi-(i+2)=0,化为(b2-b+2)+(btanθ+1)i=0,
∵b2-b+2=$(b-\frac{1}{2})^{2}$+$\frac{7}{4}$>0,因此b2-b+2=0无实数根,这与假设矛盾,
∴假设不成立,
因此原命题成立.
点评 本题考查了复数的有关知识、反证法等,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.将函数y=sinx的图象向左平移$\frac{π}{12}$个单位,然后将图象所有点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),则所得函数解析式为( )
| A. | $y=sin(\frac{1}{2}x+\frac{π}{12})$ | B. | $y=sin(\frac{1}{2}x-\frac{π}{12})$ | C. | $y=sin(2x+\frac{π}{12})$ | D. | $y=sin(2x-\frac{π}{6})$ |
5.设集合M={x|x2+x-6<0},N={x|1≤x≤3},则M∩(∁RN)等于( )
| A. | (-2,1) | B. | (-2,3] | C. | (-3,1) | D. | (-1,2] |
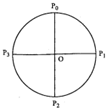 如图圆O是半径为1的圆,点PO、P1、P2、P3将圆4等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3)的取值集合是{-1,0,1}.
如图圆O是半径为1的圆,点PO、P1、P2、P3将圆4等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3)的取值集合是{-1,0,1}.