题目内容
15．已知集合A={y|y=x2-2x-3}，集合B={y|y=-x2+2x+13}，则A∩B=[-4，14]．分析 求出A与B中y的范围确定出A与B，找出两集合的交集即可．
解答 解：由A中y=x2-2x-3=x2-2x+1-4=（x-1）2-4≥-4，得到A=[-4，+∞）；
由B中y=-x2+2x+13=-（x-1）2+14≤14，得到B=（-∞，14]，
则A∩B=[-4，14]，
故答案为：[-4，14]
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．数列{an}满足a1=1，且对于任意的n∈N*都满足an+1=$\frac{{a}_{n}}{3{a}_{n}+1}$，则数列{anan+1}的前n项和为 （ ）
| A． | $\frac{1}{3n+1}$ | B． | $\frac{n}{3n+1}$ | C． | $\frac{1}{3n-2}$ | D． | $\frac{n}{3n-2}$ |
6．下列命题中，正确是（ ）
| A． | 两个向量相等，则它们的起点相同，终点也相同 | |
| B． | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| C． | 四边形ABCD中，一定有$\overrightarrow{AB}$=$\overrightarrow{DC}$ | |
| D． | 若$\overrightarrow{m}$=$\overrightarrow{n}$，$\overrightarrow{n}$=$\overrightarrow{p}$，则$\overrightarrow{m}$=$\overrightarrow{p}$ |
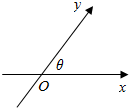如图，数轴x，y的交点为O，夹角为θ，与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1}，\overrightarrow{e_2}$．由平面向量基本定理，对于平面内的任一向量$\overrightarrow{OP}$，存在唯一的有序实数对（x，y），使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$，我们把（x，y）叫做点P在斜坐标系xOy中的坐标（以下各点的坐标都指在斜坐标系xOy中的坐标）．