题目内容
若函数f(x)=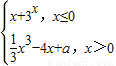 在其定义域R上有且只有一个零点,则实数a的取值范围是 .
在其定义域R上有且只有一个零点,则实数a的取值范围是 .
【答案】分析:根据函数的单调性画出函数的图象,及题意其定义域R上有且只有一个零点,即可求出a的取值范围.
解答:解:①当x≤0时,f(x)=x+3x.
∵函数y=x与y=3x在x≤0时都单调递增,
∴函数f(x)=x+3x在区间(-∞,0]上也单调递增.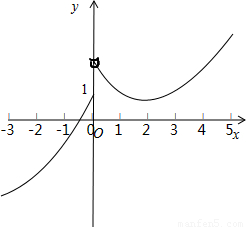
又f(-1)=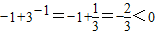 ,f(0)=1>0,所以函数f(x)在(-1,0)内有一个零点,如图所示.
,f(0)=1>0,所以函数f(x)在(-1,0)内有一个零点,如图所示.
②当x>0时,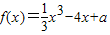 .
.
∴f′(x)=x2-4=(x+2)(x-2).
令f′(x)=0,且x>0,解得x=2.
当0<x<2时,f′(x)<0;当x>2时,f′(x)>0.
∴函数f(x)在区间(0,2)上单调递减;在区间(2,+∞)上单调递增.
∴函数f(x)在x=2时求得极小值,也即在x>0时的最小值.
∵函数f(x)在其定义域R上有且只有一个零点,且由(1)可知在区间(-1,0)内已经有一个零点了,所以在区间(0,+∞)上没有零点,
∴必须满足f(2)>0,即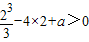 ,解得
,解得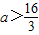 .
.
故a的取值范围是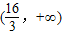 .
.
故答案为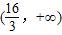 .
.
点评:利用导数得出函数的单调性并画出图象是解题的关键.
解答:解:①当x≤0时,f(x)=x+3x.
∵函数y=x与y=3x在x≤0时都单调递增,
∴函数f(x)=x+3x在区间(-∞,0]上也单调递增.

又f(-1)=
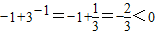 ,f(0)=1>0,所以函数f(x)在(-1,0)内有一个零点,如图所示.
,f(0)=1>0,所以函数f(x)在(-1,0)内有一个零点,如图所示.②当x>0时,
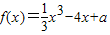 .
.∴f′(x)=x2-4=(x+2)(x-2).
令f′(x)=0,且x>0,解得x=2.
当0<x<2时,f′(x)<0;当x>2时,f′(x)>0.
∴函数f(x)在区间(0,2)上单调递减;在区间(2,+∞)上单调递增.
∴函数f(x)在x=2时求得极小值,也即在x>0时的最小值.
∵函数f(x)在其定义域R上有且只有一个零点,且由(1)可知在区间(-1,0)内已经有一个零点了,所以在区间(0,+∞)上没有零点,
∴必须满足f(2)>0,即
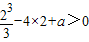 ,解得
,解得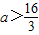 .
.故a的取值范围是
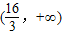 .
.故答案为
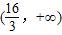 .
.点评:利用导数得出函数的单调性并画出图象是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2014•达州一模)已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
(2014•达州一模)已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).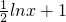 在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围
在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围 )
)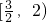
 在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围( )
在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围( ) )
)