题目内容
已知A、B、C是锐角△ABC的三个内角,向量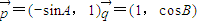 ,则
,则 的夹角是( )
的夹角是( )A.锐角
B.钝角
C.直角
D.不确定
【答案】分析:利用三角形为锐角三角形得到A+B>90°得到90°>A>90°-B>0;利用正弦函数的单调性判断出sinA>cosB;利用向量的数量积公式求出两个向量的数量积,判断出数量积小于0,判断出夹角为钝角.
解答:解:∵A、B、C是锐角△ABC的三个内角
∴A+B>90°
∴90°>A>90°-B>0
∴sinA>sin(90°-B)
即sinA>cosB
∴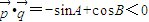
∴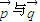 的夹角为钝角
的夹角为钝角
故选B
点评:本题考查锐角三角形三角满足的条件、考查正弦函数的单调性、考查向量的数量积公式、考查通过数量积判断向量的夹角问题.
解答:解:∵A、B、C是锐角△ABC的三个内角
∴A+B>90°
∴90°>A>90°-B>0
∴sinA>sin(90°-B)
即sinA>cosB
∴
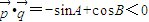
∴
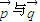 的夹角为钝角
的夹角为钝角故选B
点评:本题考查锐角三角形三角满足的条件、考查正弦函数的单调性、考查向量的数量积公式、考查通过数量积判断向量的夹角问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知A、B、C是锐角△ABC的三个内角,向量
=(-sinA,1)
=(1,cosB),则
与
的夹角是( )
| p |
| q |
| p |
| q |
| A、锐角 | B、钝角 | C、直角 | D、不确定 |