题目内容
已知A、B、C是锐角,求证:cosA+cosB+cosC=1+4sin| A |
| 2 |
| B |
| 2 |
| C |
| 2 |
分析:由题意,等式左边是和的形式,右边是乘积形式,故左边用和差化积公式,右边用积化和差公式,两边出现共同角
和
,
再提取公因式即可.
| A+B |
| 2 |
| A-B |
| 2 |
再提取公因式即可.
解答:解:cosA+cosB+cosC=1+4sin
sin
sin
?2cos
cos
=2sin2
+2sin
(-cos
+cos
)
?cos
cos
=sin2
-sin
cos
+sin
cos
?0=sin
(sin
-cos
)+(sin
-cos
)cos
?0=(sin
-cos
)(sin
+cos
)
∵A、B、C是锐角,∴sin
+cos
>0
所以上式?0=sin
-cos
?
+
=
?A+B+C=π
| A |
| 2 |
| B |
| 2 |
| C |
| 2 |
?2cos
| A+B |
| 2 |
| A-B |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
?cos
| A+B |
| 2 |
| A-B |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A+B |
| 2 |
| C |
| 2 |
| A-B |
| 2 |
?0=sin
| C |
| 2 |
| C |
| 2 |
| A+B |
| 2 |
| C |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
?0=(sin
| C |
| 2 |
| A+B |
| 2 |
| C |
| 2 |
| A-B |
| 2 |
∵A、B、C是锐角,∴sin
| C |
| 2 |
| A-B |
| 2 |
所以上式?0=sin
| C |
| 2 |
| A+B |
| 2 |
?
| C |
| 2 |
| A+B |
| 2 |
| π |
| 2 |
点评:本题考查三角恒等变形:和差化积、积化和差公式、二倍角公式、诱导公式等,考查对公式的综合运用能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知A、B、C是锐角△ABC的三个内角,向量
=(-sinA,1)
=(1,cosB),则
与
的夹角是( )
| p |
| q |
| p |
| q |
| A、锐角 | B、钝角 | C、直角 | D、不确定 |
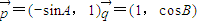 ,则
,则 的夹角是( )
的夹角是( )