题目内容
已知命题p:若a,b∈R,则|a|+|b|>1是|a+b|>1的充分不必要条件;命题q:已知A,B,C是锐角三角形ABC的三个内角;向量
=(1+sinA,1+cosA),
=(1+sinB,-1-cosB),则
与
的夹角是锐角.则( )
| m |
| n |
| m |
| n |
| A、p假q真 | B、P且q为真 |
| C、p真q假 | D、p或q为假 |
分析:分别判断两个命题的真假,再利用真值表做出选择即可,命题p可举反例说明是假命题,命题q利用向量夹角的计算公式计算即可.
解答:解:∵|-1|+|1|>1,而|-1+1|=0<1,∴命题p是假命题,
∵A,B,C是锐角三角形ABC的三个内角,∴A+B>
,即,A>
-B
∴sinA>sin(
-B),sinA>cosB,
同理,sinB>cosA,
又∵A+B>
,∴cos(A+B)<0
•
=(1+sinA)(1+sinB)+(1+cosA)(-1-cosB)=sinA+sinB-cosA-cosB-cos(A+B)>0
∴
与
的夹角是锐角,∴命题q是真命题.
故选A
∵A,B,C是锐角三角形ABC的三个内角,∴A+B>
| π |
| 2 |
| π |
| 2 |
∴sinA>sin(
| π |
| 2 |
同理,sinB>cosA,
又∵A+B>
| π |
| 2 |
| m |
| n |
∴
| m |
| n |
故选A
点评:本题考查了命题真假的判断.

练习册系列答案
相关题目
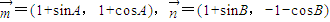 ,则
,则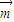 与
与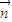 的夹角是锐角.则( )
的夹角是锐角.则( )