题目内容
已知A、B、C是锐角△ABC的三个内角,向量
=(-sinA,1)
=(1,cosB),则
与
的夹角是( )
| p |
| q |
| p |
| q |
| A、锐角 | B、钝角 | C、直角 | D、不确定 |
分析:利用三角形为锐角三角形得到A+B>90°得到90°>A>90°-B>0;利用正弦函数的单调性判断出sinA>cosB;利用向量的数量积公式求出两个向量的数量积,判断出数量积小于0,判断出夹角为钝角.
解答:解:∵A、B、C是锐角△ABC的三个内角
∴A+B>90°
∴90°>A>90°-B>0
∴sinA>sin(90°-B)
即sinA>cosB
∴
•
=-sinA+cosB<0
∴
与
的夹角为钝角
故选B
∴A+B>90°
∴90°>A>90°-B>0
∴sinA>sin(90°-B)
即sinA>cosB
∴
| p |
| q |
∴
| p |
| q |
故选B
点评:本题考查锐角三角形三角满足的条件、考查正弦函数的单调性、考查向量的数量积公式、考查通过数量积判断向量的夹角问题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
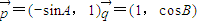 ,则
,则 的夹角是( )
的夹角是( )