题目内容
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.动直线
的左、右焦点.动直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 相交于
相交于![]() ,
,![]() 两点(直线
两点(直线![]() 与
与![]() 轴不重合).
轴不重合).

(1)若点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 坐标;
坐标;
(2)点![]() ,设直线
,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)求![]() 面积最大时的直线
面积最大时的直线![]() 的方程.
的方程.
【答案】(1) ![]() (2)见证明;(3)
(2)见证明;(3) ![]()
【解析】
(1)由已知得到直线l的方程,与椭圆方程联立即可求得点B的坐标;
(2)设直线l的方程为x=ty+1,与椭圆方程联立,利用根与系数的关系及斜率公式即可证明k1+k2=0;
(3)△AF1B的面积S![]() |F1F2||y1﹣y2|=|y1﹣y2|
|F1F2||y1﹣y2|=|y1﹣y2|![]() .把(2)中的根与系数的关系代入,可得S
.把(2)中的根与系数的关系代入,可得S .设函数f(x)=9x
.设函数f(x)=9x![]() (x≥1),利用导数可得f(x)=9x
(x≥1),利用导数可得f(x)=9x![]() 在[1,+∞)上单调递增,得到当t2+1=1,即t=0时,9(t2+1)
在[1,+∞)上单调递增,得到当t2+1=1,即t=0时,9(t2+1)![]() 取最小值10.由此可得直线l的方程为x=1.
取最小值10.由此可得直线l的方程为x=1.
(1)因为直线![]() 经过点
经过点![]() ,
,![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
由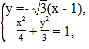 解得
解得![]() 或
或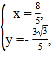
所以![]() .
.
(2)因为直线![]() 与
与![]() 轴不重合,故可设直线
轴不重合,故可设直线![]() 的方程为
的方程为![]() .
.
设![]() ,
,![]() .
.
由 得
得![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,
,![]() 在直线
在直线![]() 上,所以
上,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
从而 ![]() .
.
因为![]() ,
,
所以![]() .
.
(3)方法一:![]() 的面积
的面积![]()
![]() .
.
由(2)知,![]() ,
,![]() ,
,
故![]()
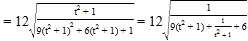 ,
,
设函数![]() .
.
因为![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() ,即
,即![]() 时,
时,![]() 取最小值10.
取最小值10.
即当![]() 时,
时,![]() 的面积取最大值,此时直线
的面积取最大值,此时直线![]() 的方程为
的方程为![]() .
.
方法二:![]() 的面积
的面积![]()
![]() .
.
由(2)知, ![]() ,
,![]() ,
,
故![]()
![]()
![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() 时,
时,![]() 的面积取最大值.
的面积取最大值.
因此,![]() 的面积取最大值时,直线
的面积取最大值时,直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目