题目内容
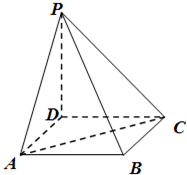如图，四棱锥P-ABCD是底面边长为1的正方形，PD⊥BC，PD=1，PC=| 2 |
（Ⅰ）求证：PD⊥面ABCD；
（Ⅱ）求二面角A-PB-D的大小．
分析：（Ⅰ）先根据边长之间的关系得到PD⊥CD；再结合PD⊥BC即可证明结论；
（Ⅱ）连接BD，设BD交AC于点O，过O作OE⊥PB于点E，连接AE，证得∠AEO就是二面角A-PB-D的平面角，最后通过求边长即可求出结果．
（Ⅱ）连接BD，设BD交AC于点O，过O作OE⊥PB于点E，连接AE，证得∠AEO就是二面角A-PB-D的平面角，最后通过求边长即可求出结果．
解答：解；（Ⅰ）证明：∵PD=DC=1，PC=
，
∴△PDC是直角三角形，即PD⊥CD，…（2分）
又∵PD⊥BC，BC∩CD=C，
∴PD⊥面ABCD…（7分）
（Ⅱ）解：连接BD，设BD交AC于点O，
过O作OE⊥PB于点E，连接AE，
∵PD⊥面ABCD，∴AO⊥PD，
又∵AO⊥BD，∴AO⊥面PDB．
∴AO⊥PB，
又∵OE⊥PB，OE∩AO=O，
∴PB⊥平面AEO，从而PB⊥EO，
故∠AEO就是二面角A-PB-D的平面角．…（10分）
∵PD⊥面ABCD，∴PD⊥BD，
∴在Rt△PDB中，PB=
=
=
，
又∵
=
，∴OE=
，…（12分）
tan∠AEO=
=
=
，∴∠AEO=60°．
故二面角A-PB-D的大小为60°．…（15分）
| 2 |
∴△PDC是直角三角形，即PD⊥CD，…（2分）
又∵PD⊥BC，BC∩CD=C，
∴PD⊥面ABCD…（7分）
（Ⅱ）解：连接BD，设BD交AC于点O，
过O作OE⊥PB于点E，连接AE，
∵PD⊥面ABCD，∴AO⊥PD，
又∵AO⊥BD，∴AO⊥面PDB．
∴AO⊥PB，
又∵OE⊥PB，OE∩AO=O，
∴PB⊥平面AEO，从而PB⊥EO，
故∠AEO就是二面角A-PB-D的平面角．…（10分）
∵PD⊥面ABCD，∴PD⊥BD，
∴在Rt△PDB中，PB=
| PD2+BD2 |
| 1+2 |
| 3 |
又∵
| OE |
| PD |
| OB |
| PB |
| ||
| 6 |
tan∠AEO=
| AO |
| OE |
| ||||
|
| 3 |
故二面角A-PB-D的大小为60°．…（15分）
点评：本题主要考察二面角的平面角及其求法以及线面垂直的证明．一般在证明线面垂直时，常先证明线线垂直，进而得线面垂直．
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=