题目内容
(12分)已知函数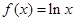 ,
,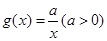 ,设
,设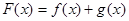 .
.
(1)求 的单调区间;
的单调区间;
(2)若以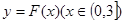 图象上任意一点
图象上任意一点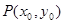 为切点的切线的斜率
为切点的切线的斜率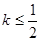
恒成立,求实数 的最小值.
的最小值.
(3)是否存在实数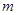 ,使得函数
,使得函数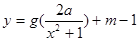 的图象与
的图象与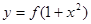 的图
的图
象恰好有四个不同的交点?若存在,求出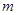 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
【答案】
(1) 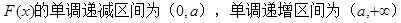
(2)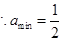 .(3)
.(3)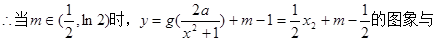

【解析】
试题分析:(1)由题意可知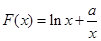 然后直接求导,利用导数大(小)于零求其单调增(减)区间即可.
然后直接求导,利用导数大(小)于零求其单调增(减)区间即可.
(2)  图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率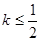
恒成立,其实质是 恒成立.即
恒成立.即
(3)解本小题的关键是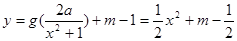 的图象与
的图象与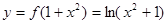 的图象恰有四个不同交点,即
的图象恰有四个不同交点,即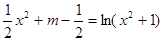 有四个不同的根,
有四个不同的根,
也就是 有四个不同的根,然后再构造函数
有四个不同的根,然后再构造函数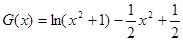
利用导数研究G(x)的单调区间,极值,画出草图,从图像上观察直线y=m在什么范围内有四个不同的交点即可.
(1) 
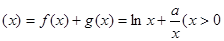


由 .
.

(2)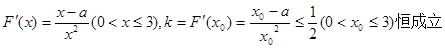
 当
当
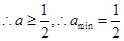 .
.
(3)若 的图象与
的图象与
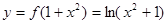 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即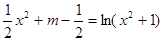 有四个不同的根,亦即
有四个不同的根,亦即
 有四个不同的根.
有四个不同的根.
令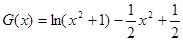 ,
,
则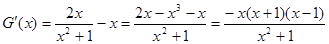 .
.
当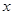 变化时
变化时 的变化情况如下表:
的变化情况如下表:
|
|
|
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1, |
|
|
+ |
0 |
- |
0 |
+ |
0 |
- |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
极大值 |
↘ |
由表格知 ,
,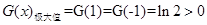 .
.
画出草图和验证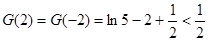 可知,当
可知,当 时,
时,


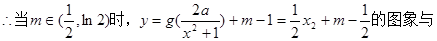

考点:导数在研究单调区间,极值,最值当中的应用.
点评:本大题综合性难度大,解决好第(2)(3)问的关键在于转化二字,第(2)问可以转化为 恒成立进一步转化一元二次函数最值问题.第(3)问关键是
恒成立进一步转化一元二次函数最值问题.第(3)问关键是 的图象与
的图象与 的图象恰有四个不同交点转化为
的图象恰有四个不同交点转化为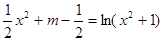 有四个不同的根,进一步转化为
有四个不同的根,进一步转化为 有四个不同的根,然后再构造函数,利用导数研究极值最值,画出图像即可解决。
有四个不同的根,然后再构造函数,利用导数研究极值最值,画出图像即可解决。

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 )
)



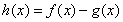

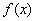

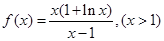
 为函数
为函数 的极值点,求证:
的极值点,求证: 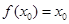 ;
;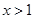 时,
时,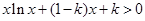 恒成立,求正整数
恒成立,求正整数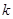 的最大值.
的最大值. 和
和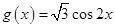 ,设动直线
,设动直线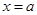 分别与
分别与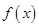 、
、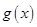 交于A,B两点,则
交于A,B两点,则 的最大值为
的最大值为
 其中
其中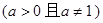 ,
,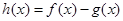 .
. 的定义域,判断
的定义域,判断 ,求使
,求使 成立的
成立的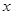 的集合
的集合