题目内容
已知函数 .
.
(Ⅰ)设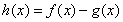 ,求
,求 的最小值;
的最小值;
(Ⅱ)如何上下平移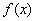 的图象,使得
的图象,使得 的图象有公共点且在公共点处切线相同.
的图象有公共点且在公共点处切线相同.
【答案】
(Ⅰ) 1;(Ⅱ)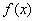 的图象向下平移1个单位后,两函数图象在公共点(1,0)处有相同的切线
的图象向下平移1个单位后,两函数图象在公共点(1,0)处有相同的切线
【解析】
试题分析:(Ⅰ)先求导,再求导数等于0的根,解导数大于0、小于0的不等式得函数的单调区间。根据函数单调性求其最值。(Ⅱ)令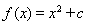 ,
,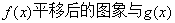 的图象有公共点即
的图象有公共点即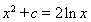 有解。公共点处切线相同.因为切点为同一点只需斜率相等即可。由导数的几何意义可知在切点处的导数就是在切点处切线的斜率,所以只需两函数在切点处导数相等。解方程组即可求出
有解。公共点处切线相同.因为切点为同一点只需斜率相等即可。由导数的几何意义可知在切点处的导数就是在切点处切线的斜率,所以只需两函数在切点处导数相等。解方程组即可求出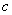 。
。
试题解析:(Ⅰ)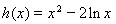 ,则
,则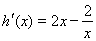 , 2分
, 2分
令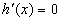 解得
解得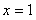 , 3分
, 3分
因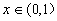 时,
时,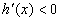 ,当
,当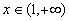 时,
时,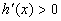 , 5分
, 5分
所以当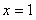 时,
时,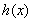 达到最小,
达到最小,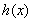 的最小值为1. 7分
的最小值为1. 7分
(Ⅱ)设上下平移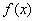 的图象为c个单位的函数解析式为
的图象为c个单位的函数解析式为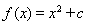 .
.
设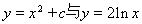 的公共点为
的公共点为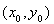 .
.
依题意有: 10分
10分
解得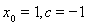 ,
,
即将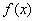 的图象向下平移1个单位后,两函数图象在公共点(1,0)处有相同的切线. 13分
的图象向下平移1个单位后,两函数图象在公共点(1,0)处有相同的切线. 13分
考点:1导数、导数的几何意义;2利用导数研究函数性质。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 的值域.
的值域.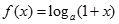 ,
,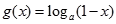 ,
,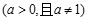 .
.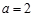 ,函数
,函数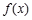 的定义域为
的定义域为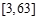 ,求函数
,求函数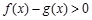 的
的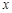 的取值范围.
的取值范围. 定义域为
定义域为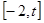 (
(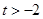 ),设
),设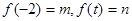 .
.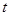 的取值范围,使得函数
的取值范围,使得函数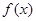 在
在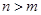 ;
;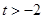 ,总存在
,总存在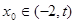 ,满足
,满足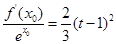 ,并确定这样的
,并确定这样的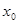 的个数.
的个数.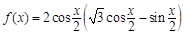 .
.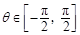 ,且
,且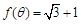 ,求
,求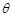 的值;
的值;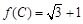 ,且△ABC的面积为
,且△ABC的面积为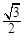 ,求sinA+sinB的值.
,求sinA+sinB的值. .
. 在
在 上单调递增,求
上单调递增,求 的取值范围。
的取值范围。 与
与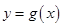 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求 轴的垂线分别与
轴的垂线分别与 的图像和
的图像和 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作 ,以T为切点作
,以T为切点作 .是否存在实数
.是否存在实数