题目内容
设动点P在直线x=1上,O为坐标原点,以OP为直角边、点O为直角顶点作等腰直角△OPQ,则动点Q的轨迹是( )
| A．圆 | B．两条平行直线 |
| C．抛物线 | D．双曲线 |
B
【思路点拨】设动点P的纵坐标t为参数,来表示|OP|=|OQ|,
·
=0,并消去参数得轨迹方程,从而确定轨迹.
设P(1,t),Q(x,y),
由题意知|OP|=|OQ|,
∴1+t2=x2+y2, ①
又·=0,∴x+ty=0,
∴t=-
,y≠0. ②
把②代入①,得(x2+y2)(y2-1)=0,即y=±1.
所以动点Q的轨迹是两条平行直线.
·=0,并消去参数得轨迹方程,从而确定轨迹.设P(1,t),Q(x,y),
由题意知|OP|=|OQ|,
∴1+t2=x2+y2, ①
又
·=0,∴x+ty=0,∴t=-
,y≠0. ②把②代入①,得(x2+y2)(y2-1)=0,即y=±1.
所以动点Q的轨迹是两条平行直线.
练习册系列答案
相关题目
并且和
轴的正半轴、
轴的正半轴所围成的三角形的面积是
的直线方程.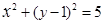
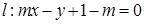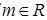，直线
.
，直线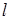
与圆C总有两个不同的交点；
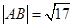，求
x+
且垂直于直线
的直线
的方程为 ．
，则直线l的方程为________．