题目内容
已知数列 满足
满足 ,
, ,(
,( )
)
(1)若 ,数列
,数列 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;
(2)若 ,试写出
,试写出 对任意
对任意 成立的充要条件,并证明你的结论.
成立的充要条件,并证明你的结论.
 满足
满足 ,
, ,(
,( )
)(1)若
 ,数列
,数列 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;(2)若
 ,试写出
,试写出 对任意
对任意 成立的充要条件,并证明你的结论.
成立的充要条件,并证明你的结论.(1)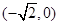 ∪
∪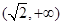 ;(2)充要条件为
;(2)充要条件为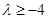 .
.
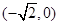 ∪
∪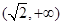 ;(2)充要条件为
;(2)充要条件为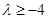 .
.试题分析:本题主要考查数列的递推公式、数列的单调性、充要条件、数学归纳法等基础知识,考查学生的分析问题解决问题的能力、计算能力、逻辑推理能力.第一问,数列
 单调递增
单调递增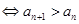 ,将已知条件代入,得到
,将已知条件代入,得到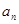 所满足条件,即
所满足条件,即 需要满足的条件,即得到a的取值范围,第二问,必要性:法一:由
需要满足的条件,即得到a的取值范围,第二问,必要性:法一:由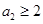 直接解出
直接解出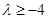 ,法二:利用已知的递推公式得到
,法二:利用已知的递推公式得到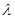 与
与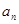 的关系,再利用配方法得到
的关系,再利用配方法得到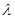 的最小值,充分性:用数学归纳法证明.
的最小值,充分性:用数学归纳法证明.试题解析:(1)若
 ,则
,则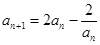 ,
,由
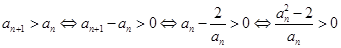 ,
,得
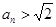 或
或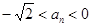 ,所以只需
,所以只需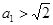 或
或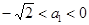 .
.所以实数
 的取值范围为
的取值范围为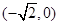 ∪
∪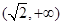 . 6分
. 6分(2)
 对任意
对任意 成立的充要条件为
成立的充要条件为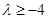 .必要性:由
.必要性:由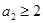 ,解出
,解出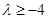 ;
;(另解:假设
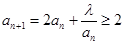 ,得
,得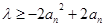 ,令
,令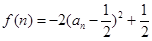 ,
, ,可得:
,可得: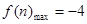 ,即有
,即有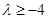 .) 8分
.) 8分充分性:数学归纳法证明:
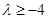 时,对一切
时,对一切 ,
, 成立.
成立.证明:(1)显然
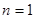 时,结论成立;
时,结论成立;(2)假设
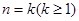 时结论成立,即
时结论成立,即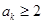 ,
,当
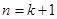 时,
时,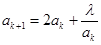 .
.考察函数
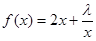 ,
, ,
,①若
 ,由
,由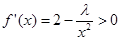 ,知
,知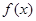 在区间
在区间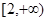 上单调递增.由假设
上单调递增.由假设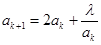
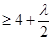
 .
.②若
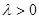 ,对
,对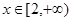 总有
总有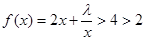 ,
,则由假设得
 .
.所以,
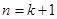 时,结论成立,
时,结论成立,综上可知:当
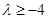 时,对一切
时,对一切 ,
, 成立.
成立.故
 对任意
对任意 成立的充要条件是
成立的充要条件是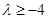 .
.
练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
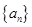 是首项和公比均为
是首项和公比均为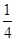 的等比数列,设
的等比数列,设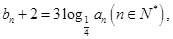 .
.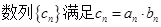
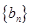 是等差数列;
是等差数列;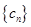 的前n项和
的前n项和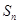 .
. 中,
中, ,对任意的
,对任意的 ,
, 、
、 、
、 成等比数列,公比为
成等比数列,公比为 ;
; 成等差数列,公差为
成等差数列,公差为 ,且
,且 .
. ,求数列
,求数列 的通项公式;
的通项公式; 的前
的前 项和
项和 .
. 的图像与直线
的图像与直线 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为 的等差数列.
的等差数列. 和
和 的值;
的值; ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若 是函数
是函数 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求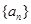 是公差不为0的等差数列,
是公差不为0的等差数列,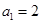 ,且
,且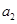 ,
,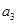 ,
,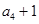 成等比数列.
成等比数列.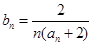 ,求数列
,求数列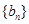 的前
的前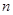 项和
项和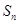 。
。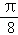 的等差数列,f(a1)+f(a2)+…+f(a8)=11π,则
的等差数列,f(a1)+f(a2)+…+f(a8)=11π,则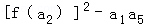 =( )
=( ) 0
0 


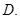
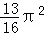
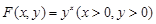 ,已知数列
,已知数列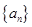 满足:
满足:
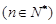 ,若对任意正整数
,若对任意正整数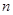 ,都有
,都有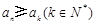 ,则
,则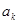 的值为
的值为  是等差数列,若
是等差数列,若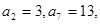 则数列
则数列 中,已知
中,已知 ,则
,则 ( )
( )


