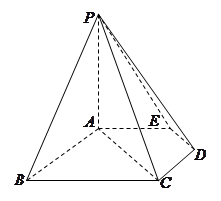题目内容
如图,四棱锥 的底面
的底面 是正方形,棱
是正方形,棱 底面
底面 ,
, =1,
=1, 是
是 的中点.
的中点.

(1)证明平面 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
 的底面
的底面 是正方形,棱
是正方形,棱 底面
底面 ,
, =1,
=1, 是
是 的中点.
的中点.
(1)证明平面
 平面
平面 ;
; (2)求二面角
 的余弦值.
的余弦值.(1)详见解析.(2)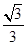
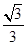
试题分析:(1) 由
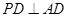 ,
,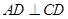 推出
推出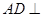 底面
底面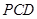 ,进而推出
,进而推出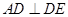 ,结合
,结合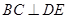 可得
可得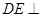 底面
底面 ,得平面
,得平面 平面
平面 ;(2)取CD的中点F,连接AC与BD,交点为M,取DM的中点N,连接EN,FN,易知
;(2)取CD的中点F,连接AC与BD,交点为M,取DM的中点N,连接EN,FN,易知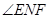 为二面角
为二面角 的平面角,在
的平面角,在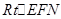 中,求出该余弦值.
中,求出该余弦值.试题解析:证明:(1) ∵
 ,
,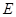 是
是 的中点, ∴
的中点, ∴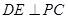 .
.∵
 底面
底面 ,∴
,∴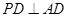 .又由于
.又由于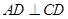 ,
,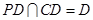 ,故
,故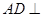 底面
底面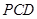 ,
,所以有
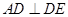 .又由题意得
.又由题意得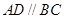 ,故
,故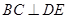 .
.
于是,由
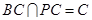 ,
,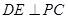 ,
,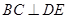 可得
可得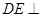 底面
底面 .
.故可得平面
 平面
平面
(2)取CD的中点F,连接AC与BD,交点为M,取DM的中点N,连接EN,FN,易知
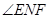 为二面角
为二面角 的平面角,又
的平面角,又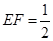 ,
, ,由勾股定理得
,由勾股定理得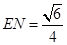 ,在
,在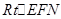 中,
中,
所以二面角
 的余弦值为
的余弦值为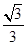 (用空间向量做,答案正确也给6分)
(用空间向量做,答案正确也给6分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的正方形
的正方形 和等腰直角三角形
和等腰直角三角形 按图拼为新的几何图形,
按图拼为新的几何图形, 中,
中, ,连结
,连结 ,若
,若 ,
, 为
为 中点
中点
 与
与 所成角的大小;
所成角的大小; 为
为 中点,证明:
中点,证明: 平面
平面 ;
; 平面
平面
 中,
中, ,点
,点 在边
在边 上,点
上,点 在边
在边 上,且
上,且 ,垂足为
,垂足为 ,若将
,若将 沿
沿 折起,使点
折起,使点 位于
位于 位置,连接
位置,连接 ,
, 得四棱锥
得四棱锥 .
.
 ;
; ,直线
,直线 与平面
与平面 所成角的大小为
所成角的大小为 ,求直线
,求直线 与平面
与平面 中,
中,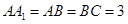 ,
,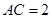 ,
,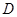 是
是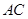 的中点.
的中点.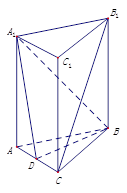
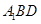 平面
平面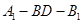 的余弦值.
的余弦值.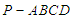 中,底面
中,底面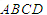 为菱形,
为菱形,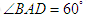 ,
,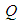 为
为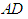 的中点。
的中点。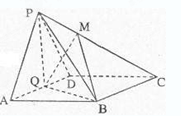
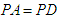 ,求证:平面
,求证:平面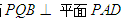 ;
;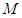 在线段
在线段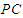 上,
上,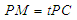 ,试确定
,试确定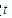 的值,使
的值,使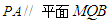 ;
;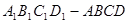 中,
中,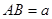 ,
,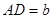 ,
,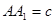 ,
,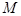 是线段
是线段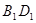 的中点.
的中点.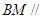 平面
平面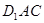 ;
;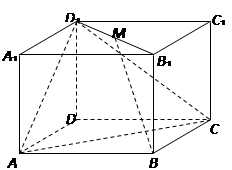
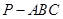 中,
中,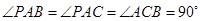 .
.
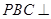 平面
平面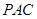 ;
;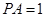 ,
,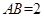 ,当三棱锥
,当三棱锥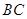 的长.
的长. 为异面直线,
为异面直线, ,
,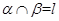 ,则直线
,则直线 ( )
( )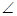 ABC=
ABC=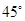 ,AB=2
,AB=2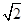 ,BC=2AE=4,
,BC=2AE=4,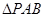 是等腰三角形.
是等腰三角形.