题目内容
复数z1=sinx+i,z2=1+i•cosx(x∈R)在坐标平面中对应的点分别是A,B,若函数f(x)=
•
(O为坐标原点),则下列命题正确的是( )
| OA |
| OB |
分析:由题设知f(x)=sinx+cosx=
sin(x+
).故f(x)的最大值为
;f(x)=
sin(x+
)的图象向左移动
个单位,得到的函数f(x)=
cosx是偶函数;y=|f(x)|的周期为π;f(x)的图象向左平移
后对应函数f(x)=
cosx图象关于x=0对称.
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
解答:解:∵复数z1=sinx+i,z2=1+i•cosx(x∈R)在坐标平面中对应的点分别是A,B,
∴A(sinx,1),B(1,cosx),
∵f(x)=
•
(O为坐标原点),
∴f(x)=sinx+cosx=
sin(x+
).
∴f(x)的最大值为
,故A不正确;
f(x)=
sin(x+
)的图象向左移动
个单位,
得到的函数f(x)=
cosx是偶函数,故B不正确;
∵f(x)=
sin(x+
),∴y=|f(x)|的周期为π,故C不正确;
∵f(x)=
sin(x+
),
∴f(x)的图象向左平移
后对应函数f(x)=
cosx图象关于x=0对称,故D正确.
故选D.
∴A(sinx,1),B(1,cosx),
∵f(x)=
| OA |
| OB |
∴f(x)=sinx+cosx=
| 2 |
| π |
| 4 |
∴f(x)的最大值为
| 2 |
f(x)=
| 2 |
| π |
| 4 |
| π |
| 4 |
得到的函数f(x)=
| 2 |
∵f(x)=
| 2 |
| π |
| 4 |
∵f(x)=
| 2 |
| π |
| 4 |
∴f(x)的图象向左平移
| π |
| 4 |
| 2 |
故选D.
点评:本题考查命题的真假判断,是基础题.解题时要注意向量、三角函数等知识点的灵活运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
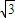 cosx)i(λ,m,x∈R),且z1=z2.
cosx)i(λ,m,x∈R),且z1=z2.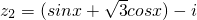 (λ,x∈R,i为虚数单位).
(λ,x∈R,i为虚数单位).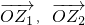 ,若
,若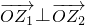 ,且λ=f(x),求f(x)的最小正周期和单调递减区间.
,且λ=f(x),求f(x)的最小正周期和单调递减区间.