题目内容
已知复数z1=sinx+λi,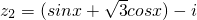 (λ,x∈R,i为虚数单位).
(λ,x∈R,i为虚数单位).
(1)若2z1=z2i,且x∈(0,π),求x与λ的值;
(2)设复数z1,z2在复平面上对应的向量分别为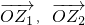 ,若
,若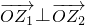 ,且λ=f(x),求f(x)的最小正周期和单调递减区间.
,且λ=f(x),求f(x)的最小正周期和单调递减区间.
解:(1)由2z1=z2i,可得 ,又λ,x∈R,
,又λ,x∈R,
∴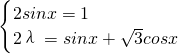 又x∈(0,π),
又x∈(0,π),
故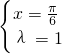 或
或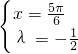 .
.
(2)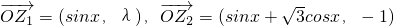 ,
,
由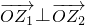 ,可得
,可得 ,
,
又λ=f(x),故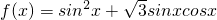 =
=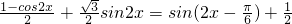 ,
,
故f(x)的最小正周期T=π,
又由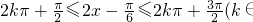 Z),可得
Z),可得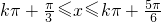 ,
,
故f(x)的单调递减区间为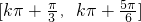 (k∈Z).
(k∈Z).
分析:(1)利用复数的运算法则和复数相等及特殊角的三角函数值即可得出;
(2)利用向量的垂直与数量积的关系可得可得 ,再利用倍角公式和两角和差的正弦公式即可化简,利用三角函数的周期公式和单调性即可得出.
,再利用倍角公式和两角和差的正弦公式即可化简,利用三角函数的周期公式和单调性即可得出.
点评:熟练掌握复数的运算法则和复数相等及特殊角的三角函数值、向量的垂直与数量积的关系、倍角公式和两角和差的正弦公式、三角函数的周期公式和单调性是解题的关键..
 ,又λ,x∈R,
,又λ,x∈R,∴
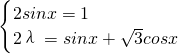 又x∈(0,π),
又x∈(0,π),故
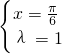 或
或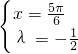 .
.(2)
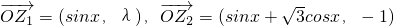 ,
,由
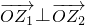 ,可得
,可得 ,
,又λ=f(x),故
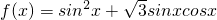 =
=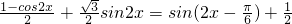 ,
,故f(x)的最小正周期T=π,
又由
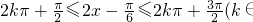 Z),可得
Z),可得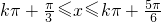 ,
,故f(x)的单调递减区间为
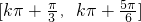 (k∈Z).
(k∈Z).分析:(1)利用复数的运算法则和复数相等及特殊角的三角函数值即可得出;
(2)利用向量的垂直与数量积的关系可得可得
 ,再利用倍角公式和两角和差的正弦公式即可化简,利用三角函数的周期公式和单调性即可得出.
,再利用倍角公式和两角和差的正弦公式即可化简,利用三角函数的周期公式和单调性即可得出.点评:熟练掌握复数的运算法则和复数相等及特殊角的三角函数值、向量的垂直与数量积的关系、倍角公式和两角和差的正弦公式、三角函数的周期公式和单调性是解题的关键..

练习册系列答案
相关题目