题目内容
已知复数z1=sinx+λi,z2=m+(m-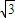 cosx)i(λ,m,x∈R),且z1=z2.
cosx)i(λ,m,x∈R),且z1=z2.(I)若λ=0,且0<x<π,求x的值;
(II)设f(x)=λcosx,求f(x)的最小正周期和单调递减区间.
【答案】分析:(I)利用两个复数相等的充要条件求得tanx=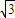 ,再由 0<x<π 可得 x的值.
,再由 0<x<π 可得 x的值.
(II)由z1=z2 可得 λ=sinx-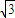 cosx,再利用三角函数的恒等变换化简函数的解析式为sin(2x-
cosx,再利用三角函数的恒等变换化简函数的解析式为sin(2x-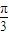 )-
)-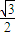 ,由此求得函数 f(x)的最小正周期,由 2kπ+
,由此求得函数 f(x)的最小正周期,由 2kπ+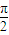 ≤2x-
≤2x-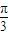 ≤2kπ+
≤2kπ+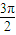 ,
,
k∈z,求得x的范围,即可得到f(x)的单调递减区间.
解答:解:(I)若λ=0,且0<x<π,由z1=z2 可得 m=sinx,m-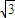 cosx=0,
cosx=0,
∴sinx-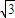 cosx=0,tanx=
cosx=0,tanx=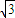 .再由 0<x<π 可得 x=
.再由 0<x<π 可得 x=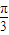 .
.
(II)由z1=z2 可得 m=sinx,m- cosx=λ,∴λ=sinx-
cosx=λ,∴λ=sinx-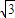 cosx,
cosx,
∴f(x)=λcosx=(sinx-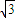 cosx )cosx=
cosx )cosx=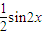 -
-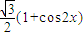 =sin(2x-
=sin(2x-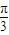 )-
)-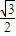 ,
,
故函数 f(x)的最小正周期等于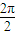 =π.
=π.
由 2kπ+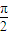 ≤2x-
≤2x- ≤2kπ+
≤2kπ+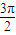 ,k∈z,可得 kπ+
,k∈z,可得 kπ+ ≤x≤kπ+
≤x≤kπ+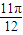 ,k∈z.
,k∈z.
故f(x)的单调递减区间为[kπ- ,kπ+
,kπ+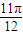 ],k∈z.
],k∈z.
点评:本题主要考查两个复数相等的充要条件,三角函数的恒等变换及化简求值,正弦函数的周期性和单调性,化简函数的解析式为sin(2x-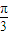 )-
)-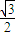 ,是解题的关键,属于中档题.
,是解题的关键,属于中档题.
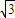 ,再由 0<x<π 可得 x的值.
,再由 0<x<π 可得 x的值.(II)由z1=z2 可得 λ=sinx-
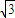 cosx,再利用三角函数的恒等变换化简函数的解析式为sin(2x-
cosx,再利用三角函数的恒等变换化简函数的解析式为sin(2x-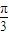 )-
)-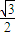 ,由此求得函数 f(x)的最小正周期,由 2kπ+
,由此求得函数 f(x)的最小正周期,由 2kπ+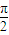 ≤2x-
≤2x-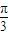 ≤2kπ+
≤2kπ+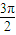 ,
,k∈z,求得x的范围,即可得到f(x)的单调递减区间.
解答:解:(I)若λ=0,且0<x<π,由z1=z2 可得 m=sinx,m-
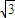 cosx=0,
cosx=0,∴sinx-
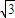 cosx=0,tanx=
cosx=0,tanx=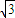 .再由 0<x<π 可得 x=
.再由 0<x<π 可得 x=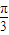 .
.(II)由z1=z2 可得 m=sinx,m-
 cosx=λ,∴λ=sinx-
cosx=λ,∴λ=sinx-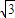 cosx,
cosx,∴f(x)=λcosx=(sinx-
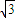 cosx )cosx=
cosx )cosx=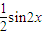 -
-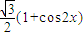 =sin(2x-
=sin(2x-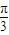 )-
)-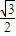 ,
,故函数 f(x)的最小正周期等于
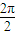 =π.
=π.由 2kπ+
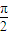 ≤2x-
≤2x- ≤2kπ+
≤2kπ+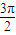 ,k∈z,可得 kπ+
,k∈z,可得 kπ+ ≤x≤kπ+
≤x≤kπ+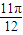 ,k∈z.
,k∈z.故f(x)的单调递减区间为[kπ-
 ,kπ+
,kπ+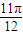 ],k∈z.
],k∈z.点评:本题主要考查两个复数相等的充要条件,三角函数的恒等变换及化简求值,正弦函数的周期性和单调性,化简函数的解析式为sin(2x-
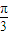 )-
)-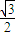 ,是解题的关键,属于中档题.
,是解题的关键,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目