题目内容
20.已知函数y=f(1-x2)的定义域[-2,3],则函数g(x)=$\frac{f(2x+1)}{x+2}$的定义域是( )| A. | (-∞,-2)∪(-2,3] | B. | [-8,-2)∪(-2,1] | C. | [-$\frac{9}{2}$,-2)∪(-2,0] | D. | [-$\frac{9}{2}$,-2] |
分析 函数y=f(1-x2)的定义域[-2,3],可得-2≤x≤3,可得-8≤1-x2≤1.由$\left\{\begin{array}{l}{-8≤2x+1≤1}\\{x+2≠0}\end{array}\right.$,解出即可.
解答 解:∵函数y=f(1-x2)的定义域[-2,3],
∴-2≤x≤3,
∴-8≤1-x2≤1
由$\left\{\begin{array}{l}{-8≤2x+1≤1}\\{x+2≠0}\end{array}\right.$,
解得$-\frac{9}{2}≤x≤0$,且x≠-2.
故选:C.
点评 本题考查了函数的定义域的求法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.在△ABC中,角A,B,C的对边分别为a,b,c,cos2$\frac{A}{2}$=$\frac{b+c}{2c}$,则△ABC的形状一定是( )
| A. | 正三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
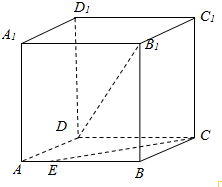 如图,正方体ABCD-A1B1C1D1的棱长为1,点E在棱AB上,且AE=m.已知异面直线DB1与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$,求m的值.
如图,正方体ABCD-A1B1C1D1的棱长为1,点E在棱AB上,且AE=m.已知异面直线DB1与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$,求m的值.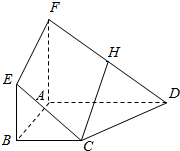 如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.
如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.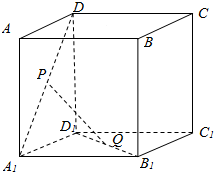 如图,正方体的棱长为a,P、Q分别为A1D、B1D1的中点
如图,正方体的棱长为a,P、Q分别为A1D、B1D1的中点