ƒøƒĞ»ı
÷±œşABπ˝≈◊ŒÔœşx2=2py£®p£æ0£©µƒΩπµ„F£¨≤¢”Î∆‰œ‡Ωª”ĞA°¢B¡Ωµ„£¨Q «œş∂ŒABµƒ÷–µ„£¨M «≈◊ŒÔœşµƒ◊ºœş”Îy÷·µƒΩªµ„£¨O «◊¯±Í‘≠µ„£Æ£®¢Ò£©«Û
| MA |
| MB |
£®¢Ú£©π˝A°¢B¡Ωµ„∑÷±◊˜¥À≈◊ŒÔœşµƒ«–œş£¨¡Ω«–œşœ‡Ωª”ĞNµ„£¨«Û÷§£∫
| MN |
| OF |
| NQ |
| OF |
£®¢Û£©»Ùp «≤ªŒ™1µƒ’˝’˚ ˝£¨µ±
| MA |
| MB |
| 5 |
| 5 |
∑÷Œˆ£∫£®¢Ò£©”…ú˛µ√M£®0£¨-
£©£¨F£®0£¨
£©£Æ…Ë÷±œşABµƒ∑Ω≥ÃŒ™y=kx+
£¨A£®x1£¨y1£©£¨B£®x2£¨y2£©£¨‘Úx12=2py1£¨x22=2py2£¨Q£®
£¨
£©£Æ”…
µ√x2-2pkx-p2=0£Æ”…Œ§¥Ô∂®¿ÌƒİπªÕ∆µº≥ˆ
•
µƒ»°÷µ∑∂Œß£Æ
£®¢Ú£©≈◊ŒÔœş∑Ω≥Ãø…ªØŒ™y=
x2£¨«Ûµºµ√y=
x£ÆkNA=y
£¨kNB®Ty
£Æ«–œşNAµƒ∑Ω≥ÃŒ™£∫y-
=
(x-x1)£¨«–œşNBµƒ∑Ω≥ÃŒ™£∫y=
x-
£Æ”…
Ω‚µ√N£®
£¨
£©£¨¥”∂¯ø…÷™Nµ„Qµ„µƒ∫·◊¯±Íœ‡Õ¨µ´◊ı◊¯±Í≤ªÕ¨£Æ”…¥Àƒİπª÷§√˜
•
=0£¨
°Œ
£Æ
£®¢Û£©”…
•
=4p2£Æ”÷∏˘æı
•
=p2k2£¨÷™4p2=p2k2£¨∂¯p£æ0£¨k2=4£¨k=°¿2£Æ”…
=£®-pk£¨p£©£¨
=(x2-x1£¨y2-y1) =(x2-x1)(1+
=£®x2-x1£©£®1£¨k£©£¨÷™
•
=(-pk£¨p)(x2-x1) (1£¨k)=(x2-x1) (-pk-pk)=0£¨¥”∂¯
°Õ
£Æ”…¥Àƒİπª«Û≥ˆ≈◊ŒÔœşµƒ∑Ω≥ãÆ
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
|
| MA |
| MB |
£®¢Ú£©≈◊ŒÔœş∑Ω≥Ãø…ªØŒ™y=
| 1 |
| 2p |
| 1 |
| p |
| x1 |
| p |
| x2 |
| p |
| x12 |
| 2p |
| x1 |
| p |
| x2 |
| p |
| x22 |
| 2p |
|
| x1+x2 |
| 2 |
| x1x2 |
| 2p |
| MN |
| OF |
| NQ |
| OF |
£®¢Û£©”…
| MA |
| MB |
| MA |
| MB |
| NF |
| AB |
| x1+x2 ) |
| 2p |
| NF |
| AB |
| NF |
| AB |
Ω‚¥£∫Ω‚£∫£®¢Ò£©”…ú˛µ√M£®0£¨-
£©£¨F£®0£¨
£©£Æ…Ë÷±œşABµƒ∑Ω≥ÃŒ™
y=kx+
£¨A£®x1£¨y1£©£¨B£®x2£¨y2£©
‘Úx12=2py1£¨x22=2py2£¨Q£®
£¨
£©£Æ£®2∑÷£©
”…
µ√x2-2pkx-p2=0£Æ
°‡”…Œ§¥Ô∂®¿Ìµ√x1+x2=2pk£¨x1•x2=-p2£®3∑÷£©
¥”∂¯”–y1y2=
=
£¨y1+y2=k£®x1+x2£©+p=2pk2+p£Æ
°‡
•
µƒ»°÷µ∑∂Œß «[0£¨+°Ş£©£Æ£®4∑÷£©
£®¢Ú£©≈◊ŒÔœş∑Ω≥Ãø…ªØŒ™y=
x2£¨«Ûµºµ√y=
x£Æ
°‡kNA=y
£¨kNB®Ty
£Æ
°‡«–œşNAµƒ∑Ω≥ÃŒ™£∫y-
=
(x-x1)º¥y=
x-
£Æ
«–œşNBµƒ∑Ω≥ÃŒ™£∫y=
x-
£®6∑÷£©
”…
Ω‚µ√
°‡N£®
£¨
£©
¥”∂¯ø…÷™Nµ„Qµ„µƒ∫·◊¯±Íœ‡Õ¨µ´◊ı◊¯±Í≤ªÕ¨£Æ
°‡NQ°ŒOF£Æº¥
°Œ
£®7∑÷£©
”÷”…£®¢Ò£©÷™x1+x2=2pk£¨x1•x2=-p2£¨
°‡N£®pk£¨-
£©£Æ£®8∑÷£©
∂¯M£®0£¨-
£©°‡
=(pk£¨0)
”÷
=(0£¨
)£Æ°‡
•
=0£Æ£®9∑÷£©
£®¢Û£©”…
•
=4p2£Æ”÷∏˘æı£®¢Ò£©÷™
•
=p2k2
°‡4p2=p2k2£¨∂¯p£æ0£¨°‡k2=4£¨k=°¿2£Æ£®10∑÷£©
”…”Ğ
=£®-pk£¨p£©£¨
=(x2-x1£¨y2-y1) =(x2-x1)(1+
=£®x2-x1£©£®1£¨k£©
°‡
•
=(-pk£¨p)(x2-x1) (1£¨k)=(x2-x1) (-pk-pk)=0
¥”∂¯
°Õ
£Æ£®11∑÷£©
”÷|
|=
=
p£¨|
|=y1+y2+p=2pk2-2p=10p£¨
°‡S°˜ABN=
|NF||AB|=
°¡
p°¡10p=5
p2£Æ
∂¯S°˜ABNµƒ»°÷µ∑∂Œß «[5
£¨20
]£Æ
°‡5
°İ5
£¨p2°İ20
£¨1°İp2°İ4£Æ£®13∑÷£©
∂¯p£æ0£¨°‡1°İp°İ2£Æ
”÷p «≤ªŒ™1µƒ’˝’˚ ˝£Æ
°‡p=2£Æ
π ≈◊ŒÔœşµƒ∑Ω≥ã∫x2=4y£Æ£®14∑÷£©£Æ
| p |
| 2 |
| p |
| 2 |
y=kx+
| p |
| 2 |
‘Úx12=2py1£¨x22=2py2£¨Q£®
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
”…
|
°‡”…Œ§¥Ô∂®¿Ìµ√x1+x2=2pk£¨x1•x2=-p2£®3∑÷£©
¥”∂¯”–y1y2=
| x12x22 |
| 4p2 |
| p2 |
| 4 |
°‡
| MA |
| MB |
£®¢Ú£©≈◊ŒÔœş∑Ω≥Ãø…ªØŒ™y=
| 1 |
| 2p |
| 1 |
| p |
°‡kNA=y
| x1 |
| p |
| x2 |
| p |
°‡«–œşNAµƒ∑Ω≥ÃŒ™£∫y-
| x12 |
| 2p |
| x1 |
| p |
| x1 |
| p |
| x12 |
| 2p |
«–œşNBµƒ∑Ω≥ÃŒ™£∫y=
| x2 |
| p |
| x22 |
| 2p |
”…
|
|
| x1+x2 |
| 2 |
| x1x2 |
| 2p |
¥”∂¯ø…÷™Nµ„Qµ„µƒ∫·◊¯±Íœ‡Õ¨µ´◊ı◊¯±Í≤ªÕ¨£Æ
°‡NQ°ŒOF£Æº¥
| NQ |
| OF |
”÷”…£®¢Ò£©÷™x1+x2=2pk£¨x1•x2=-p2£¨
°‡N£®pk£¨-
| p |
| 2 |
∂¯M£®0£¨-
| p |
| 2 |
| MN |
”÷
| OF |
| p |
| 2 |
| MN |
| OF |
£®¢Û£©”…
| MA |
| MB |
| MA |
| MB |
°‡4p2=p2k2£¨∂¯p£æ0£¨°‡k2=4£¨k=°¿2£Æ£®10∑÷£©
”…”Ğ
| NF |
| AB |
| x1+x2 ) |
| 2p |
°‡
| NF |
| AB |
¥”∂¯
| NF |
| AB |
”÷|
| NF |
| p2k2+p2 |
| 5 |
| AB |
°‡S°˜ABN=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∂¯S°˜ABNµƒ»°÷µ∑∂Œß «[5
| 5 |
| 5 |
°‡5
| 5 |
| 5 |
| 5 |
∂¯p£æ0£¨°‡1°İp°İ2£Æ
”÷p «≤ªŒ™1µƒ’˝’˚ ˝£Æ
°‡p=2£Æ
π ≈◊ŒÔœşµƒ∑Ω≥ã∫x2=4y£Æ£®14∑÷£©£Æ
µ„∆¿£∫±æÂøº≤È ˝¡øª˝µƒ»°÷µ∑∂Œß°¢œÚ¡ø∆Ω––∫Õ¥π÷±µƒ÷§√˜°¢≈◊ŒÔœş∑Ω≥õƒ«Û∑®£¨Ω‚ ±“™»œ’Ê…Û£¨◊¢“‚Œ§¥Ô∂®¿Ì°¢µº ˝–‘÷ °¢œÚ¡ø‘ÀÀ„∫Õ懿Îπ´ Ωµƒ¡ÈªÓ‘À”√£Æ

¡∑œ∞≤·œµ¡–¥∞∏
œ‡πÿƒø
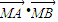 µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª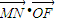 =0£¨
=0£¨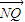 °Œ
°Œ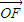 £ª
£ª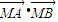 =4P2£¨°˜ABNµƒ√ʪ˝µƒ»°÷µ∑∂ŒßŒ™[5
=4P2£¨°˜ABNµƒ√ʪ˝µƒ»°÷µ∑∂ŒßŒ™[5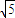 £¨20
£¨20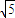 ] ±£¨«Û∏√≈◊ŒÔœşµƒ∑Ω≥ãÆ
] ±£¨«Û∏√≈◊ŒÔœşµƒ∑Ω≥ãÆ