题目内容
5. 两个半径分别为r1,r2的圆M,N,公共弦AB长为3,如图所示,则$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=9.
两个半径分别为r1,r2的圆M,N,公共弦AB长为3,如图所示,则$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=9.
分析 可连接MN,从而可知MN⊥AB,且平分AB,设MN与AB交于O,则有$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=$2\overrightarrow{AO}•\overrightarrow{AB}$,根据$|\overrightarrow{AO}|=\frac{3}{2},|\overrightarrow{AB}|=3$便可求出$\overrightarrow{AO}•\overrightarrow{AB}$,从而得出答案.
解答 解:如图,连接MN,交AB于O,则MN⊥AB,且MN把AB平分;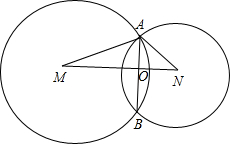
∴$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=$(\overrightarrow{AO}+\overrightarrow{OM})•\overrightarrow{AB}+(\overrightarrow{A0}+\overrightarrow{ON})•\overrightarrow{AB}$
=$\overrightarrow{AO}•\overrightarrow{AB}+0+\overrightarrow{AO}•\overrightarrow{AB}+0$
=$2\overrightarrow{AO}•\overrightarrow{AB}=2×\frac{3}{2}×3=9$.
故答案为:9.
点评 考查两圆心的连线垂直且平分相交弦,向量加法的几何意义,向量垂直的充要条件,以及向量数量积的计算公式.

练习册系列答案
相关题目
14.在△ABC中,tanA是以-4为第4项、4为第8项的等差数列{an}的公差,tanB是以$\frac{1}{3}$为第2项、9为第5项的等比数列{bn}的公比,则△ABC是( )
| A. | 钝角三角形 | B. | 等腰直角三角形 | C. | 锐角三角形 | D. | 以上都不对 |
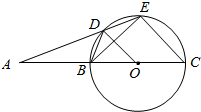 已知圆O,点A为圆O外一点,BC为圆O的直径,过A作圆O的割线交圆O于D,E两点,其满足BD=DE.
已知圆O,点A为圆O外一点,BC为圆O的直径,过A作圆O的割线交圆O于D,E两点,其满足BD=DE.