题目内容
17.建造一个容积为8m3、深2m的长方体无盖水池,池底任一边长度不得小于1m,如果池底和池壁的造价分别为120元/m2和80元/m2,总造价y(元)关于底面一边x(m)的函数解析式为f(x).(1)求函数f(x)的解析式,并求出该函数的定义域;
(2)x取何值时,总造价最低?
分析 (1)通过水池的容积及深度可知水池底面面积为4m2,利用“总造价=池底造价+池壁造价”计算即得结论;
(2)利用基本不等式可知x+$\frac{4}{x}$≥4当且仅当x=2时取等号,进而计算可得结论.
解答 解:(1)依题意可知水池底面面积为$\frac{8}{2}$=4m2,
则f(x)=120×4+80×2(2x+2×$\frac{4}{x}$)
=480+320(x+$\frac{4}{x}$),
∵池底任一边长度不得小于1m,
∴$\left\{\begin{array}{l}{x≥1}\\{\frac{4}{x}≥1}\end{array}\right.$,即该函数的定义域为{x|1≤x≤4};
(2)∵x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,当且仅当x=$\frac{4}{x}$即x=2时取等号,
∴当x=2时总造价最低为480+320(2+$\frac{4}{2}$)=1760元.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于基础题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
7.12个同类产品中含有2个次品,现从中任意抽出3个,必然事件是( )
| A. | 3个都是正品 | B. | 至少有一个是次品 | ||
| C. | 3个都是次品 | D. | 至少有一个是正品 |
 两个半径分别为r1,r2的圆M,N,公共弦AB长为3,如图所示,则$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=9.
两个半径分别为r1,r2的圆M,N,公共弦AB长为3,如图所示,则$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=9.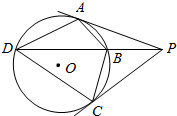 如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证:
如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证: