计算$\sqrt{4-\sqrt{15}}$+$\sqrt{4+\sqrt{15}}$．题目和参考答案——青夏教育精英家教网—

题目内容

13．计算$\sqrt{4-\sqrt{15}}$+$\sqrt{4+\sqrt{15}}$．

分析化简可得4-$\sqrt{15}$=$\frac{8-2\sqrt{15}}{2}$=$\frac{（\sqrt{5}-\sqrt{3}）^{2}}{2}$，4+$\sqrt{15}$=$\frac{（\sqrt{5}+\sqrt{3}）^{2}}{2}$，从而解得．

解答解：4-$\sqrt{15}$=$\frac{8-2\sqrt{15}}{2}$=$\frac{（\sqrt{5}-\sqrt{3}）^{2}}{2}$，
同理，4+$\sqrt{15}$=$\frac{（\sqrt{5}+\sqrt{3}）^{2}}{2}$，
故$\sqrt{4-\sqrt{15}}$+$\sqrt{4+\sqrt{15}}$
=$\frac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}$+$\frac{\sqrt{5}+\sqrt{3}}{\sqrt{2}}$
=2$\frac{\sqrt{5}}{\sqrt{2}}$=$\sqrt{10}$．

点评本题考查了完全平方式的应用及根式的化简与运算．

练习册系列答案

初中毕业学业考试模拟试卷湖南教育出版社系列答案

4．若关于x的二次方程x²-2mx+（m-1）=0有且仅有一个正实根，则实数m的取值范围是m≤1．

1．设a=1.1^0.9，b=0.9^1.1，c=log_1.10.9，则a，b，c的大小关系是（　　）

8．如果实数x，y满足等式（x-2）²+y²=3，那么x²+y²的最大值是7+4$\sqrt{3}$．

3．事件A，B，C相互独立，若P（A•B）=$\frac{1}{6}$，P（$\overline{B}$•C）=$\frac{1}{8}$，P（A•B•$\overline{C}$）=$\frac{1}{8}$，则P（B）=$\frac{1}{2}$．

10．已知tanα=1，3sinβ=sin（2α+β），求tan（α+β）的值．

7．下列命题中正确的是（　　）

	A．	两两相交的三条直线共面
	B．	两条相交直线上的三个点可以确定一个平面
	C．	梯形是平面图形
	D．	一条直线和一个点可以确定一个平面

8．

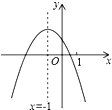二次函数y=ax²+bx+c（a≠0）的图象如图，给出下列四个结论：
①4ac-b²＜0；
②4a+c＜2b；
③3b+2c＜0；
④m（am+b）+b＜a（m≠-1），
其中正确结论的个数是（　　）

试题分类