题目内容
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1个该产品获利润5元,未售出的产品,每个亏损3元.根据历史资料,得到开学季市场需求量的频率分布直方图如图所示.该同学为这个开学季购进了160个该产品,以![]() (
(![]() ,单位:个)表示这个开学季内的市场需求量.
,单位:个)表示这个开学季内的市场需求量.
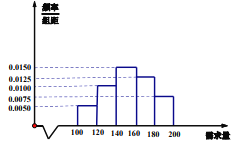
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)根据直方图估计利润不少于640元的概率.
【答案】(1)![]() ;(2)0.7.
;(2)0.7.
【解析】试题分析:(1)利用频率分布直方图得到需求量![]() 的中位数;(2)利用频率分布直方图估计利润不少于640元的概率.
的中位数;(2)利用频率分布直方图估计利润不少于640元的概率.
试题解析:
(1)需求量的中位数为![]() ,则根据直方图知
,则根据直方图知![]()
∴![]()
解得: ![]()
(2)设利润不少于640元为事件![]() ,
,
当![]() 时,利润为:
时,利润为: ![]() ,
,
当![]() 时,利润为:
时,利润为: ![]()
由![]() ,解得:
,解得: ![]()
∴根据直方图![]() 的估计值为:
的估计值为: ![]()
∴利润不少于640元的概率为0.7.
点睛: 利用频率分布直方图求众数、中位数与平均数时,易出错,应注意区分这三者.在频率分布直方图中:(1)最高的小长方形底边中点的横坐标即是众数;(2)中位数左边和右边的小长方形的面积和是相等的;(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目