题目内容
已知双曲线 -
- =1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A, B两点,O为坐标原点. 若双曲线的离心率为2, △AOB的面积为
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A, B两点,O为坐标原点. 若双曲线的离心率为2, △AOB的面积为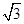 , 则p=( )
, 则p=( )
| A.1 | B.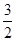 |
| C.2 | D.3 |
C
解析

练习册系列答案
相关题目
抛物线 上的一点M到焦点的距离为1,则点M到y轴的距离是 ( )
上的一点M到焦点的距离为1,则点M到y轴的距离是 ( )
A. | B. |
| C.1 | D. |
顶点在原点,准线与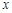 轴垂直,且经过点
轴垂直,且经过点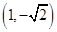 的抛物线方程是( )
的抛物线方程是( )
A.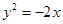 | B.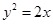 | C.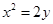 | D.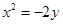 |
椭圆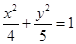 的一个焦点坐标是( )
的一个焦点坐标是( )
A.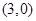 | B.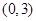 | C.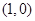 | D.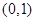 |
抛物线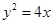 的焦点坐标为( )
的焦点坐标为( )
| A.(2,0) | B.(1,0) | C.(0,-4) | D.(-2,0) |
设P是双曲线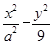 =1左支上一点,该双曲线的一条渐近线方程是3x+4y=0,F1,F2分别是双曲线的左、右焦点,若|PF1|=10,则|PF2|等于( )
=1左支上一点,该双曲线的一条渐近线方程是3x+4y=0,F1,F2分别是双曲线的左、右焦点,若|PF1|=10,则|PF2|等于( )
| A.2 | B.2或18 | C.18 | D.16 |
已知F1,F2分别是双曲线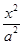 -
-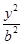 =1(a>0,b>0)的左、右焦点,P为双曲线右支上的任意一点.若
=1(a>0,b>0)的左、右焦点,P为双曲线右支上的任意一点.若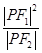 =8a,则双曲线的离心率的取值范围是( )
=8a,则双曲线的离心率的取值范围是( )
| A.(1,2] | B.[2,+∞) |
| C.(1,3] | D.[3,+∞) |
若抛物线y2=2px的焦点与双曲线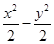 =1的右焦点重合,则p的值为( )
=1的右焦点重合,则p的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
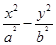 =1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( ).
=1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( ).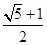
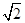 +1
+1 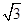 +1
+1