题目内容
如图是一个从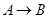 的”闯关”游戏.
的”闯关”游戏. 
规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于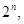 则闯关成功.
则闯关成功.
(1)求闯第一关成功的概率;
(2)记闯关成功的关数为随机变量X,求X的分布列和期望。
(1) P= .
.
(2) X的分布列为 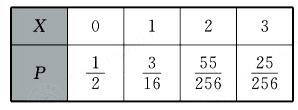
EX=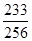
解析试题分析:(1)抛一次正四面体面朝下的数字有1,2,3,4四种情况,大于2的有两种情况,故闯第一关成功的概率为P= .
.
(2)记事件”抛掷n次正四面体,这n次面朝下的数字之和大于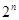 ”为事件
”为事件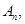 则
则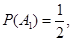 抛掷两次正四面体面朝下的数字之和的情况如图所示,易知
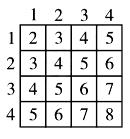
抛掷两次正四面体面朝下的数字之和的情况如图所示,易知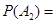
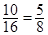 .
.
设抛掷三次正四面体面朝下的数字依次记为:x,y,z,
考虑x+y+z>8的情况,当x=1时,y+z>7有1种情况;
当x=2时,y+z>6有3种情况;当x=3时,y+z>5有6种情况;
当x=4时,y+z>4有10种情况.
故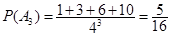 .
.
由题意知,X的所有可能取值为0,1,2,3.
P(X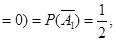
P(X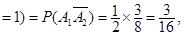
P(X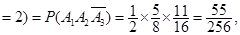
P(X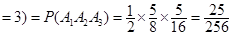 .
.
∴X的分布列为 
EX=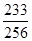
考点:古典概型概率的计算,独立事件同时发生的概率公式,随机变量的分布列及其期望。
点评:中档题,本题综合性较强,综合考查了古典概型概率的计算,独立事件同时发生的概率公式,随机变量的分布列及其期望。在(II)小题的解答中,注意就x+y+z的不同取值情况加以分析,易错易漏,应高度注意。此类问题比较典型,对计算能力、分析问题解决问题的能力要求较高。是高考题中的“应用问题”。

练习册系列答案
相关题目
 小时收费
小时收费 元,超过
元,超过 元(不足
元(不足 小时.
小时. 小时的概率为
小时的概率为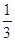 ,停车付费多于
,停车付费多于 元的概率为
元的概率为 ,求甲停车付费恰为
,求甲停车付费恰为 元的概率.
元的概率. 为摸出两球中白球的个数,
为摸出两球中白球的个数,
 ,且他们是否译出密码互不影响。
,且他们是否译出密码互不影响。 、
、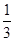 、
、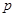 ,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为 .
.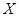 ,求
,求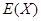 .
. ,其中:
,其中: ,记函数
,记函数 满足条件:
满足条件: 的事件为A,求事件A发生的概率。
的事件为A,求事件A发生的概率。