题目内容
【题目】设函数![]() .已知曲线
.已知曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极值点;
的极值点;
(3)若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,函数
时,函数![]() 有一个极小值点
有一个极小值点![]() 和一个极大值点
和一个极大值点![]() ,当
,当![]() 时,函数
时,函数![]() 在
在![]() 上有无极值点,当
上有无极值点,当![]() 时,函数
时,函数![]() 有唯一的极大值点
有唯一的极大值点![]() ,无极小值点;(3)
,无极小值点;(3)![]() .
.
【解析】
试题(1)根据导数的几何意义求出曲线![]() 在点
在点![]() 处的切线斜率,利用两直线垂直时斜率间的关系即可求得
处的切线斜率,利用两直线垂直时斜率间的关系即可求得![]() 的值;(2)因为
的值;(2)因为![]() ,其极值点就是
,其极值点就是![]() 在
在![]() 上的变号零点的个数,通过讨论对称轴的位置和判别式
上的变号零点的个数,通过讨论对称轴的位置和判别式![]() 的符合得其单调性,找到函数
的符合得其单调性,找到函数![]() 的极值点情况;(3)要使总存在
的极值点情况;(3)要使总存在![]() ,使得
,使得![]() 成立,即总存在
成立,即总存在![]() ,使得
,使得![]() 成立,构造函数
成立,构造函数![]() ,
,![]() ,则总存在
,则总存在![]() ,使得
,使得![]() 成立,所以即
成立,所以即![]() ,利用导数研究含
,利用导数研究含![]() 的单调性,求出最大值和最小值即得
的单调性,求出最大值和最小值即得![]() 的范围.
的范围.
试题解析:(1)![]() ,
,
所以![]() ,所以
,所以![]() ,
,
(2)![]() ,其定义域为
,其定义域为![]() ,
,
![]() ,
,
令![]() ,
,
![]()
①当![]() 时,
时,![]() ,有
,有![]() ,即
,即![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减,故
上单调递减,故![]() 在区间
在区间![]() 无极值点;
无极值点;
②当![]() 时,
时,![]() ,令
,令![]() ,有
,有![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,得
,得![]() 在
在![]() 上递减;
上递减;
当![]() 时,
时,![]() ,即
,即![]() ,得
,得![]() 在
在![]() 上递增;
上递增;
当![]() 时,
时,![]() ,即
,即![]() ,得
,得![]() 在
在![]() 上递减;
上递减;
此时![]() 有一个极小值点
有一个极小值点![]() 和一个极大值点
和一个极大值点![]() .
.
③当![]() 时,
时,![]() ,
,
令![]() ,有
,有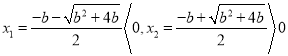 ,
,
当![]() 时,
时,![]() ,即
,即![]() ,得
,得![]() 在
在![]() 上递增;
上递增;
当![]() 时,
时,![]() ,即
,即![]() ,得
,得![]() 在
在![]() 上递减.
上递减.
此时![]() 唯一的极大值点
唯一的极大值点![]() ,无极小值点,
,无极小值点,
综上可知,当![]() 时,函数
时,函数![]() 有一个极小值点
有一个极小值点![]() 和一个极大值点
和一个极大值点![]() .
.
当![]() 时,函数
时,函数![]() 在
在![]() 上有无极值点;
上有无极值点;
当![]() 时,函数
时,函数![]() 有唯一的极大值点
有唯一的极大值点![]() ,无极小值点
,无极小值点
(3)令![]() ,
,![]() ,
,
则![]() ,
,
若总存在![]() ,使得
,使得![]() 成立,
成立,
即总存在![]() ,使得
,使得![]() 成立,
成立,
即总存在![]() ,使得
,使得![]() 成立,
成立,
即![]() ,
,
![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
即![]() 对任意
对任意![]() 成立,
成立,
即![]() 对任意
对任意![]() 成立,
成立,
构造函数:![]() ,
,![]() ,
,
![]() ,当
,当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() .
.
∴对于任意![]() ,∴
,∴![]() .
.
所以![]()

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目