题目内容
(1)试画出由方程
=
所确定的函数y=f(x)图象.
(2)若函数y=ax+
与y=f(x)的图象恰有一个公共点,求a的取值范围.
lg(6-x)+lg(x-2)+lo
| ||||
| lg2y |
| 1 |
| 2 |
(2)若函数y=ax+
| 1 |
| 2 |
分析:(1)通过方程确定x,y的范围,然后化简方程为函数画出函数的图象即可.
(2)通过直线y=ax+
经过点A(2,8)时,直线y=ax+
经过点B(5,
)时,求出a的范围,说明直线y=ax+
与f(x) 的图象也恰有一个公共点.直线y=ax+
与上述抛物线BC弧有一切点,求出a.
(2)通过直线y=ax+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: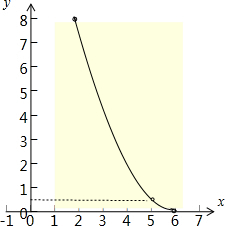 解:(1)易知x∈(2,6),y≠
解:(1)易知x∈(2,6),y≠
.原方程可变为lg(6-x)=
lg2y,由此得y=
(x-6)2.注意到y≠
,
故函数y=f(x)=
(x-6)2,x∈(2,5)∪(5,6),其中图象是抛物线的一部分.
(2)当直线y=ax+
经过点A(2,8)时,a=
,当直线
y=ax+
经过点B(5,
)时,a=0,故当0<a<
时
与抛物线的AB弧恰有一个公共点.
同理,当-
≤a<0时,直线y=ax+
与f(x) 的图象也恰有一个公共点.
此外,直线y=ax+
与上述抛物线BC弧有一切点,其横坐标为
,此时a=
-6.
综上所述,a的取值范围为[-
,0)∪(0,
)∪{
-6}.
 解:(1)易知x∈(2,6),y≠
解:(1)易知x∈(2,6),y≠| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故函数y=f(x)=
| 1 |
| 2 |
(2)当直线y=ax+
| 1 |
| 2 |
| 15 |
| 4 |
y=ax+
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
与抛物线的AB弧恰有一个公共点.
同理,当-
| 1 |
| 12 |
| 1 |
| 2 |
此外,直线y=ax+
| 1 |
| 2 |
| 35 |
| 35 |
综上所述,a的取值范围为[-
| 1 |
| 12 |
| 15 |
| 4 |
| 35 |
点评:本题考查函数的图象,函数与方程关系,函数的定义域与值域,分类讨论思想与数形结合知识,考查分析问题解决问题的能力,容易出现定义域遗漏,直线与方程的交点讨论不全的情况.

练习册系列答案
相关题目
 (2012•黄浦区二模)如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.
(2012•黄浦区二模)如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.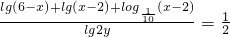 所确定的函数y=f(x)图象.
所确定的函数y=f(x)图象. 与y=f(x)的图象恰有一个公共点,求a的取值范围.
与y=f(x)的图象恰有一个公共点,求a的取值范围.
 所确定的函数y=f(x)图象.
所确定的函数y=f(x)图象. 与y=f(x)的图象恰有一个公共点,求a的取值范围.
与y=f(x)的图象恰有一个公共点,求a的取值范围.