题目内容
如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.(1)试画出该几何体的三视图;(主视图投影面平行平面DCC1D1,主视方向如图所示.请将三张视图按规定位置画在答题纸的相应虚线框内)
(2)若截面△MNH是边长为2的正三角形,求该几何体的体积V.

【答案】分析:(1)根据三视图的定义可画出该几何体的三视图
(2)由正三角形△MNH是的边长,先求出截掉的三棱锥的棱长和体积,用正方体的体积减掉小三棱锥的体积即可
解答:解(1)
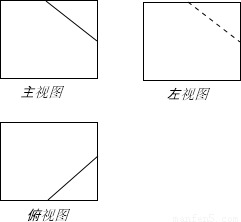
(2)设原正方体中由顶点B1出发的三条棱的棱长分别为B1M=x,B1N=y,B1H=z.
结合题意,可知,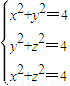 ,解得
,解得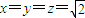 .
.
因此,所求几何体的体积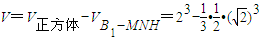 =
=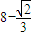
点评:本题考查由三视图求面积、体积,求解的关键是由视图得出几何体的长、宽、高等性质,熟练掌握各种类型的几何体求体积的公式是关键
(2)由正三角形△MNH是的边长,先求出截掉的三棱锥的棱长和体积,用正方体的体积减掉小三棱锥的体积即可
解答:解(1)

(2)设原正方体中由顶点B1出发的三条棱的棱长分别为B1M=x,B1N=y,B1H=z.
结合题意,可知,
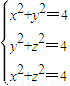 ,解得
,解得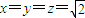 .
.因此,所求几何体的体积
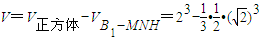 =
=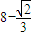
点评:本题考查由三视图求面积、体积,求解的关键是由视图得出几何体的长、宽、高等性质,熟练掌握各种类型的几何体求体积的公式是关键

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 (2012•浦东新区一模)如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.
(2012•浦东新区一模)如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体. (2012•黄浦区二模)如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.
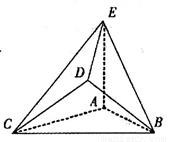
(2012•黄浦区二模)如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体. 是边长为2的正三角形. 若
是边长为2的正三角形. 若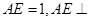 平面
平面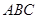 ,平面
,平面 平面
平面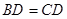 ,且
,且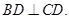
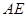 //平面
//平面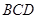 ;
; 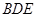
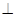 平面
平面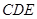 .
. 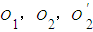 分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.
分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点. 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).