题目内容
2.已知函数f(x)=lnx-ax+$\frac{{x}^{2}}{2}$.(1)若f(x)为定义域内的单调函数,求实数a的取值范围;
(2)判断函数f(x)的单调性;
(3)对于n∈N+,求证:4ln(n+1)<[22+($\frac{3}{2}$)2+…+($\frac{n+1}{n}$)2]-[($\frac{1}{2}$)2+($\frac{2}{3}$)2+…+($\frac{n}{n+1}$)2].
分析 (1)利用导数判断函数单调性,转化为恒成立问题,求函数的最值即可.
(2)利用(1)的结果,讨论a>2时函数的单调性即可.
(3)利用(2)函数的单调减区间,方程的根推出$4[ln(n+1)-lnn]<{(\frac{n+1}{n})}^{2}-{(\frac{n}{n+1})}^{2}$,然后利用累加法推出结果即可.
解答 解:函数f(x)=lnx-ax+$\frac{{x}^{2}}{2}$.
则函数f′(x)=$\frac{1}{x}$-a+x=$\frac{{x}^{2}-ax+1}{x}$,x>0.
(1)∵f(x)为定义域内的单调函数,∴x2-ax+1≥0恒成立.∴a$≤\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$恒成立,
∵x+$\frac{1}{x}$≥2(当且仅当x=1时取等号)∴a≤2.
(2)由(1)可知a≤2时函数是增函数,
当a>2时,x2-ax+1=0,可得${x}_{1}=\frac{a-\sqrt{{a}^{2}-4}}{2}$,${x}_{2}=\frac{a+\sqrt{{a}^{2}-4}}{2}$,
∵x1+x2=a>0,x1•x2=1,可知0<x1<1<x2,
当x∈(0,x1)时,f(x)递增,x∈[x1,x2]时,函数单调递减,x∈(x2,+∞)时,函数单调递增.
综上:a≤2时,函数的单调增区间(0,+∞).
a>2时,函数的单调增区间(0,x1)和(x2,+∞),单调减区间[x1,x2].
(3)由(2)可知,f(x)在[x1,x2],函数单调递减,则f(x1)>f(x2).
令x1=$\frac{n}{n+1}$,${x}_{2}=\frac{n+1}{n}$,可知当a=$\frac{n}{n+1}+\frac{n+1}{n}$时,x1,x2是方程x2-ax+1=0的两个根,
∴$ln\frac{n}{n+1}-(\frac{n}{n+1}+\frac{n+1}{n})•\frac{n}{n+1}+\frac{1}{2}(\frac{n}{n+1})^{2}>$$ln\frac{n+1}{n}-(\frac{n}{n+1}+\frac{n+1}{n})•\frac{n+1}{n}+\frac{1}{2}({\frac{n+1}{n})}^{2}$,
化简可得:$4[ln(n+1)-lnn]<(\frac{n+1}{n})^{2}-(\frac{n}{n+1})^{2}$,
分别令n=1,2,3,…,n-1,n,得到n个式子相加,可得
4ln(n+1)<[22+($\frac{3}{2}$)2+…+($\frac{n+1}{n}$)2]-[($\frac{1}{2}$)2+($\frac{2}{3}$)2+…+($\frac{n}{n+1}$)2].13分.
点评 本题考查函数的单调性以及函数的导数的应用,考查分类讨论以及转化思想的应用,考查分析问题解决问题的能力.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 2014年12月28日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)
2014年12月28日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)| 乘公共电汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含). |
乘坐地铁方案(不含机场线) | 6公里(含)内3元; 6公里至12公里(含)4元; 12公里至22公里(含)5元; 22公里至32公里(含)6元; 32公里以上部分,每增加1元可乘坐20公里(含). |
(Ⅰ)如果从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
(Ⅱ)已知选出的120人中有6名学生,且这6人乘坐地铁的票价情形恰好与按票价从这120人中分层抽样所选的结果相同,现从这6人中随机选出2人,求这2人的票价和恰好为8元的概率;
(Ⅲ)小李乘坐地铁从A地到陶然亭的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为s公里,试写出s的取值范围.(只需写出结论)
| A. | y=-2x | B. | y=3x | C. | y=-3x | D. | y=4x |
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | 充要条件 | B. | 充分且不必要条件 | ||
| C. | 必要且不充分条件 | D. | 既不充分也不必要条件 |
 :指数函数
:指数函数 在
在 上单调递减,命题
上单调递减,命题 :关于
:关于 的方程
的方程 的两个实根均大于
的两个实根均大于 .若
.若 或
或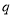 为真,
为真, 且
且 的取值范围.
的取值范围. 在角
在角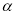 的终边上,则
的终边上,则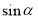 的值为( )
的值为( ) B.
B.
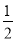 D.
D.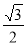
 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,侧面
,侧面 底面
底面 ,
, .
.
 平面
平面 ;
; ,求点
,求点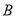 到直线
到直线 的距离.
的距离.